
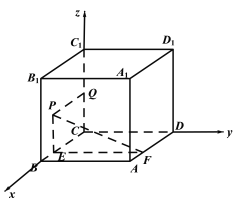
【题目】在棱长为1的正方体![]() 中,已知点P为侧面
中,已知点P为侧面![]() 上的一动点,则下列结论正确的是( )
上的一动点,则下列结论正确的是( )
A.若点P总保持![]() ,则动点P的轨迹是一条线段;
,则动点P的轨迹是一条线段;
B.若点P到点A的距离为![]() ,则动点P的轨迹是一段圆弧;
,则动点P的轨迹是一段圆弧;
C.若P到直线![]() 与直线
与直线![]() 的距离相等,则动点P的轨迹是一段抛物线;
的距离相等,则动点P的轨迹是一段抛物线;
D.若P到直线![]() 与直线
与直线![]() 的距离比为
的距离比为![]() ,则动点P的轨迹是一段双曲线.
,则动点P的轨迹是一段双曲线.
【答案】ABD
【解析】
由![]() 平面
平面![]() 且平面
且平面![]() 平面
平面![]() ,即可判断A;根据球的性质及与正方体的截面性质即可判断B;作
,即可判断A;根据球的性质及与正方体的截面性质即可判断B;作![]() ,
,![]() ,连接
,连接![]() ,作
,作![]() .建立空间直角坐标系,由
.建立空间直角坐标系,由![]() 即可求得动点P的轨迹方程,即可判断C;根据题意,由距离比即可求得轨迹方程,进而判断D.
即可求得动点P的轨迹方程,即可判断C;根据题意,由距离比即可求得轨迹方程,进而判断D.
对于A,![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,故动点P的轨迹为线段
,故动点P的轨迹为线段![]() ,所以A正确;
,所以A正确;
对于B,点P的轨迹为以A为球心、半径为![]() 的球面与面
的球面与面![]() 的交线,即为一段圆弧,所以B正确;
的交线,即为一段圆弧,所以B正确;
对于C,作![]() ,
,![]() ,连接
,连接![]() ;作
;作![]() .由
.由![]() ,在面
,在面![]() 内,以C为原点、以直线
内,以C为原点、以直线![]() 、
、![]() 、
、![]() 为x,y,z轴建立平面直角坐标系,如下图所示:
为x,y,z轴建立平面直角坐标系,如下图所示:
设![]() ,则
,则![]() ,化简得
,化简得![]() ,P点轨迹所在曲线是一段双曲线,所以C错误.
,P点轨迹所在曲线是一段双曲线,所以C错误.
对于D,由题意可知点P到点![]() 的距离与点P到直线
的距离与点P到直线![]() 的距离之比为
的距离之比为![]() ,结合C中所建立空间直角坐标系,可得
,结合C中所建立空间直角坐标系,可得![]() ,所以
,所以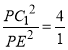 ,代入可得
,代入可得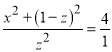 ,化简可得
,化简可得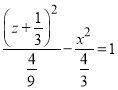 ,故点P的轨迹为双曲线,所以D正确.
,故点P的轨迹为双曲线,所以D正确.
综上可知,正确的为ABD.
故选:ABD.


科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,曲线C的参数方程为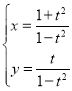 (t为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(
(t为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(![]() )
)![]() .
.
(1)求曲线C和直线l的直角坐标方程;
(2)若直线l交曲线C于A,B两点,交x轴于点P,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
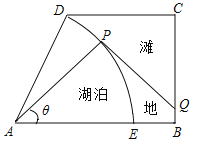
【题目】如图,某湿地公园的鸟瞰图是一个直角梯形,其中:![]() ,
,![]() ,
,![]() ,
,![]() 长1千米,
长1千米,![]() 长
长![]() 千米,公园内有一个形状是扇形的天然湖泊
千米,公园内有一个形状是扇形的天然湖泊![]() ,扇形
,扇形![]() 以
以![]() 长为半径,弧
长为半径,弧![]() 为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段
为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段![]() 线段
线段![]() 弧
弧![]() ,其中Q在线段
,其中Q在线段![]() 上(异于线段端点),
上(异于线段端点),![]() 与弧
与弧![]() 相切于P点(异于弧端点]根据市场行情
相切于P点(异于弧端点]根据市场行情![]() ,
,![]() 段的建造费用是每千米10万元,湖岸段弧
段的建造费用是每千米10万元,湖岸段弧![]() 的建造费用是每千米
的建造费用是每千米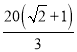 万元(步行道的宽度不计),设
万元(步行道的宽度不计),设![]() 为
为![]() 弧度观光步行道的建造费用为
弧度观光步行道的建造费用为![]() 万元.
万元.
(1)求步行道的建造费用![]() 关于
关于![]() 的函数关系式,并求其走义域;
的函数关系式,并求其走义域;
(2)当![]() 为何值时,步行道的建造费用最低?
为何值时,步行道的建造费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]() 与曲线C:
与曲线C:![]() (
(![]() ,
,![]() )交于不同的两点A,B,O为坐标原点.
)交于不同的两点A,B,O为坐标原点.
(1)若![]() ,
,![]() ,求证:曲线C是一个圆;
,求证:曲线C是一个圆;
(2)若曲线C过![]() 、
、![]() ,是否存在一定点Q,使得
,是否存在一定点Q,使得![]() 为定值?若存在,求出定点Q和定值;若不存在,请说明理由.
为定值?若存在,求出定点Q和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量AQI指数是反映空气质量状况指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI指数值 |
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图所示的是某市11月1日至20日AQI指数变化的折线图:
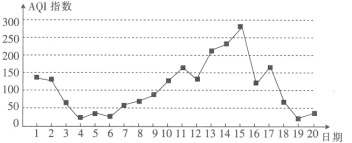
下列说法不正确的是( )
A.这![]() 天中空气质量为轻度污染的天数占
天中空气质量为轻度污染的天数占![]()
B.这![]() 天中空气质量为优和良的天数为
天中空气质量为优和良的天数为![]() 天
天
C.这![]() 天中AQI指数值的中位数略低于
天中AQI指数值的中位数略低于![]()
D.总体来说,该市11月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com