
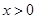 ,函数
,函数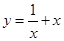 的最小值是 ( )
的最小值是 ( )| A.2 | B.4 | C.6 | D.8 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
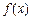 在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数
在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数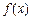 在[m,n] (m<n)上具有“DK”性质.
在[m,n] (m<n)上具有“DK”性质.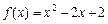 在[1,2]上是否具有“DK”性质,说明理由;
在[1,2]上是否具有“DK”性质,说明理由;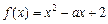 在[a,a+1]上具有“DK”性质,求a的取值范围.
在[a,a+1]上具有“DK”性质,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
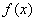 是定义在
是定义在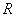 的增函数,且
的增函数,且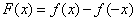 ,那么
,那么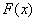 一定是
一定是A.奇函数,且在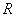 上是增函数 上是增函数 | B.奇函数,且在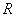 上是减函数 上是减函数 |
C.偶函数,且在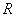 上是增函数 上是增函数 | D.偶函数,且在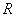 上是减函数 上是减函数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
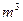 ,深为3
,深为3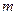 .如果池底每平方米的造价为150元,池壁每平方米的造价为
.如果池底每平方米的造价为150元,池壁每平方米的造价为 120元,怎样设计水池能使总造价最低?最低造价是多少?
120元,怎样设计水池能使总造价最低?最低造价是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com