
已知数列 的前n项和
的前n项和 且
且 =2.
=2.
(1) 求 的值,并证明:当n>2时有
的值,并证明:当n>2时有 ;
;
(2) 求证: …
… .
.
【解析】本试题主要是考查了数列中通项公式与前n项和关系式的运用。得到数列相邻两项之间的关系式。同时能利用 的通项公式,求解前n项和,并求和证明。
的通项公式,求解前n项和,并求和证明。
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| bnbn+1 |
查看答案和解析>>
科目:高中数学 来源:2011届甘肃省天水市三中高三第六次检测数学文卷 题型:解答题
、(12分)已知数列  的前n项和Sn=2n2+2n数列
的前n项和Sn=2n2+2n数列  的前 n 项和 Tn=2-bn
的前 n 项和 Tn=2-bn
(1)求数列  与
与  的通项公式;
的通项公式;
(2)设Cn=an2·bn,证明当且仅当n≥3时,Cn+1<Cn
查看答案和解析>>
科目:高中数学 来源:2013届广东省汕头市高二第一学期期末考试文科数学试卷 题型:解答题
已知数列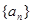 的前n项和
的前n项和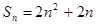 ,数列
,数列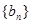 的前n项和为
的前n项和为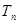 ,且
,且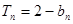
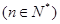 .
.
(1)求数列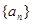 与
与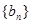 的通项公式;
的通项公式;
(2)设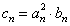 ,若
,若 <
<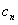 ,求
,求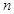 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com