
����Ŀ��ij�������÷����ʳƷ������������������ڸó�������һְ�����ᣬ����������з����䴦����������������ϵ�ѡ�������ᵽ���������йأ���������������з���![]() ����Ԫ���������빤���ľ���
����Ԫ���������빤���ľ���![]() �Ĺ�ϵΪ��
�Ĺ�ϵΪ�� ![]() ��Ϊ�˽�ͨ���㣬����������֮�仹Ҫ��һ�����ױ������֪��·ÿ����ɱ�Ϊ
��Ϊ�˽�ͨ���㣬����������֮�仹Ҫ��һ�����ױ������֪��·ÿ����ɱ�Ϊ![]() ��Ԫ������һ���Բ���ְ����ͨ��
��Ԫ������һ���Բ���ְ����ͨ��![]() ��Ԫ.��
��Ԫ.��![]() Ϊ������������·�������ְ���IJ���֮�ͣ�
Ϊ������������·�������ְ���IJ���֮�ͣ�
����![]() �ı���ʽ��
�ı���ʽ��
������Ӧ�����빤����Զ������ʹ�ܷ���![]() ��С��������Сֵ��
��С��������Сֵ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߶�ij���20����������һ����������20��������ƽ���ֳ�����С�飬��һ��͵ڶ������������ߣ���λ�� ![]() ���ľ�Ҷͼ���£�
���ľ�Ҷͼ���£�

��1�����ݾ�Ҷͼ���ֱ�д������ѧ�����ߵ���λ����
��2���Ӹð����߳���![]() ��7�����������ѡ��2�������μ�У����Ӽ�ѵ������2������������1�����Եڶ���ĸ��ʣ�
��7�����������ѡ��2�������μ�У����Ӽ�ѵ������2������������1�����Եڶ���ĸ��ʣ�
��3�������������![]() �����
����λ�� ![]() ���������и����ѡ��2�ˣ�����4��������λ��
���������и����ѡ��2�ˣ�����4��������λ��![]() ����λ��
����λ�� ![]() ��������Ϊ
��������Ϊ![]() �����������
�����������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�����ס�������Ͱװ��Ʒ����֪�����ײ�Ʒ1Ͱ���![]() ԭ��2ǧ�ˣ�
ԭ��2ǧ�ˣ� ![]() ԭ��3ǧ�ˣ������Ҳ�Ʒ1Ͱ���
ԭ��3ǧ�ˣ������Ҳ�Ʒ1Ͱ���![]() ԭ��2ǧ�ˣ�
ԭ��2ǧ�ˣ� ![]() ԭ��1ǧ�ˣ�ÿͰ�ײ�Ʒ��������300Ԫ��ÿͰ�Ҳ�Ʒ��������400Ԫ����˾��Ҫ��ÿ������
ԭ��1ǧ�ˣ�ÿͰ�ײ�Ʒ��������300Ԫ��ÿͰ�Ҳ�Ʒ��������400Ԫ����˾��Ҫ��ÿ������![]() ԭ�϶�������12ǧ�˵������£�������Ʒ
ԭ�϶�������12ǧ�˵������£�������Ʒ![]() ����Ʒ
����Ʒ![]() ������֮�͵����ֵΪ�� ��
������֮�͵����ֵΪ�� ��
A. 1800Ԫ B. 2100Ԫ C. 2400Ԫ D. 2700Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������װ��ż���������к������ռһ��.�ס��ҡ����������պ�.ÿ�δӴ�������ȡ������������һ�������У����������Ǻ��ͽ���һ��������ҺУ�����ͷ������.�ظ��������̣�ֱ������������������У���( )
A.�Һ��к����ڱ����к���
B.�Һ��к���������к���һ����
C.�Һ��к����ڱ����к���
D.�Һ��к���������к���һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ж�������Բ��λ�ù�ϵ.
(1)C1��x2��y2��2x��3��0��C2��x2��y2��4x��2y��3��0��___________
(2)C1��x2��y2��2y��0��C2��x2��y2��2![]() x��6��0��___________
x��6��0��___________
(3)C1��x2��y2��4x��6y��9��0��C2��x2��y2��12x��6y��19��0��___________
(4)C1��x2��y2��2x��2y��2��0��C2��x2��y2��4x��6y��3��0.___________
��5��x2��y2��9��x2��y2��8x��6y��9��0 ________________
��6��ԲC1��x2��y2��2x��6y��6��0��ԲC2��x2��y2��4x��2y��4��0______
��7��Բx2��y2��6x��7��0��Բx2��y2��6y��27��0 ____________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������÷����ʳƷ������������������ڸó�������һְ�����ᣬ����������з����䴦����������������ϵ�ѡ�������ᵽ���������йأ���������������з���![]() ����Ԫ���������빤���ľ���
����Ԫ���������빤���ľ���![]() �Ĺ�ϵΪ��
�Ĺ�ϵΪ�� ![]() ��Ϊ�˽�ͨ���㣬����������֮�仹Ҫ��һ�����ױ������֪��·ÿ����ɱ�Ϊ
��Ϊ�˽�ͨ���㣬����������֮�仹Ҫ��һ�����ױ������֪��·ÿ����ɱ�Ϊ![]() ��Ԫ������һ���Բ���ְ����ͨ��
��Ԫ������һ���Բ���ְ����ͨ��![]() ��Ԫ.��
��Ԫ.��![]() Ϊ������������·�������ְ���IJ���֮�ͣ�
Ϊ������������·�������ְ���IJ���֮�ͣ�
����![]() �ı���ʽ��
�ı���ʽ��
������Ӧ�����빤����Զ������ʹ�ܷ���![]() ��С��������Сֵ��
��С��������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A�� ![]() ��
�� ![]() ,��
,�� ![]() (N��2)�������С��n(2��n��N)��ÿ��������k����
(N��2)�������С��n(2��n��N)��ÿ��������k���� ![]() ��
�� ![]() �����n������A��һ����Gʱ�̡����ǡ�G��A��������A �����С�Gʱ�̡���ɵļ��ϡ�
�����n������A��һ����Gʱ�̡����ǡ�G��A��������A �����С�Gʱ�̡���ɵļ��ϡ�
��1��������A��-2��2��-1��1��3��д��G��A��������Ԫ�أ�
��2��֤����������A�д��� ![]() ʹ��
ʹ�� ![]() >
> ![]() ����G��A��
����G��A�� ![]()
![]() ��
��
��3��֤����������A���� ![]() -
- ![]() ��1��n=2,3, ��,N��,��GA����Ԫ�ظ�����С��
��1��n=2,3, ��,N��,��GA����Ԫ�ظ�����С�� ![]() -
- ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѡ���⡿�������A��B��C��D��С�⣬��ѡ��������С�⣬������Ӧ�Ĵ����������������������������ǰ��С�����֣����ʱӦд������˵����֤�����̻����㲽�裮
��1��A����ѡ��4��1����֤��ѡ����
��ͼ���ڡ�ABC�У���ABC=90�㣬BD��AC �� DΪ���㣬E��BC���е㣬��֤����EDC=��ABD.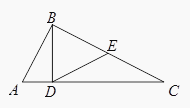
��2��B.��ѡ��4��2��������任��
��֪����A= ![]() ����B�������B��1=
����B�������B��1= 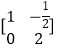 �������AB.
�������AB.
��3����ѡ��4��4������ϵ��������̡���ƽ��ֱ������ϵxOy�У���ֱ֪��l�IJ�������Ϊ 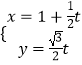 ��tΪ����������ԲC�IJ�������Ϊ
��tΪ����������ԲC�IJ�������Ϊ ![]() ��
�� ![]() Ϊ������.��ֱ��l����ԲC�ཻ��A �� B���㣬���߶�AB�ij�.
Ϊ������.��ֱ��l����ԲC�ཻ��A �� B���㣬���߶�AB�ij�.
��4��D. ��a��0��|x��1|�� ![]() ��|y��2|��
��|y��2|�� ![]() ����֤��|2x+y��4|��a��
����֤��|2x+y��4|��a��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABC��A1B1C1��A1A�͵���ABC���ҡ�ABCΪ�������Σ�A1A=AB=6��DΪAC�е㣮

��1��������C1��BCD�������
��2����֤��ƽ��BC1D��ƽ��ACC1A1��
��3����֤��ֱ��AB1��ƽ��BC1D��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com