
【题目】试比较下面概率的大小:
(1)如果以连续掷两次骰子依次得到的点数m,n作为点P的横、纵坐标,点P在直线![]() 的下面
的下面![]() 包括直线
包括直线![]() 的概率
的概率![]() ;
;
(2)在正方形![]() ,
,![]() ,x,
,x,![]() ,随机地投掷点P,求点P落在正方形T内直线
,随机地投掷点P,求点P落在正方形T内直线![]() 的下面
的下面![]() 包括直线
包括直线![]() 的概率
的概率![]() .
.
 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.

(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为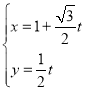 (t为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρsin2θ=4cosθ.
(t为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρsin2θ=4cosθ.
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)若直线l与x轴的交点为F,直线l与曲线C的交点为A、B,求|FA|+|FB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知点![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,它与曲线
,它与曲线![]() 的交点为
的交点为![]() ,
,![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将边长为1的正方形ABCD沿x轴正向滚动,先以A为中心顺时针旋转,当B落在x轴时,又以B为中心顺时针旋转,如此下去,设顶点C滚动时的曲线方程为![]() ,则下列说法不正确的是
,则下列说法不正确的是![]()

A.![]() 恒成立B.
恒成立B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)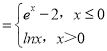 ,g(x)=f(
,g(x)=f(![]() )+1(k∈R,k≠0),则下列关于函数y=f[g(x)]+1的零点个数判断正确的是( )
)+1(k∈R,k≠0),则下列关于函数y=f[g(x)]+1的零点个数判断正确的是( )
A.当k>0时,有2个零点;当k<0时,有4个零点
B.当k>0时,有4个零点;当k<0时,有2个零点
C.无论k为何值,均有2个零点
D.无论k为何值,均有4个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,人们的支付方式发生了巨大转变,使用移动支付购买商品已成为一部分人的消费习惯.某企业为了解该企业员工![]() 、
、![]() 两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况.发现样本中
两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况.发现样本中![]() ,
,![]() 两种支付方式都没有使用过的有5人;使用了
两种支付方式都没有使用过的有5人;使用了![]() 、
、![]() 两种方式支付的员工,支付金额和相应人数分布如下:
两种方式支付的员工,支付金额和相应人数分布如下:
支付金额(元) 支付方式 |
|
| 大于2000 |
使用 | 18人 | 29人 | 23人 |
使用 | 10人 | 24人 | 21人 |
依据以上数据估算:若从该公司随机抽取1名员工,则该员工在该月![]() 、
、![]() 两种支付方式都使用过的概率为______.
两种支付方式都使用过的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解某产品的销售情况,选择某个电商平台对该产品销售情况作调查.统计了一年内的月销售数量(单位:万件),得到该电商平台月销售数量的茎叶图.
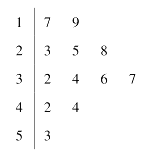
(1)求该电商平台在这一年内月销售该产品数量的中位数和平均数;
(2)该企业与电商签订销售合同时规定:如果电商平台当月的销售件数不低于40万件,当月奖励该电商平台10万元;当月低于40万件没有奖励,用该样本估计总体,从电商平台一个年度内高于该年月销售平均数的月份中任取两个月,求这两个月企业发给电商平台的奖金为20万元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com