Question

某射手射击1次，击中目标的概率是0.9。她连续射击4次，且各次射击是否击中目标相互之间没有影响.有下列结论：

①他第3次击中目标的概率是0.9；

②他恰好击中目标3次的概率是；

③他至少击中目标1次的概率是；

④他击中目标2次的概率是0.81.

其中正确结论的序号是              （写出所有正确结论的序号）

 

Answer 1

【答案】

①、③

【解析】

试题分析：由题意知射击一次击中目标的概率是0.9，得到第3次击中目标的概率是0.9，连续射击4次，且各次射击是否击中目标相互之间没有影响，得到是一个独立重复试验，根据独立重复试验的公式得到恰好击中目标3次的概率和至少击中目标1次的概率，他击中目标的次数ξ是一个二项分布，即ξ～B（4，0.9），根据二项分布的概率公式可求出Eξ．解：∵射击一次击中目标的概率是0.9，∴第3次击中目标的概率是0.9，∴①正确，∵连续射击4次，且各次射击是否击中目标相互之间没有影响，∴本题是一个独立重复试验，根据独立重复试验的公式得到恰好击中目标3次的概率是C₄³×0.9³×0.1∴②不正确，∵至少击中目标1次的概率用对立事件表示是1-0.1⁴．∴③正确，他击中目标2次的概率是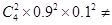0.81∴④   不正确，故答案为：①③

考点：n次独立重复试验

点评：本题主要考查n次独立重复试验中恰好发生k次的概率，以及离散型随机变量的期望，属于中档题．