
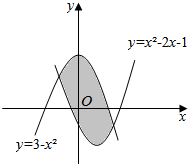
 如图,两曲线y=3-x2与y=x2-2x-1所围成的图形面积是( )
如图,两曲线y=3-x2与y=x2-2x-1所围成的图形面积是( )| A. | 6 | B. | 9 | C. | 12 | D. | 3 |
分析 依据图形得到积分从而利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可.
解答 解:对于y=3-x2,当y=0时,x=±$\sqrt{3}$,
对于y=x2-2x-1,当y=0时,x=1±$\sqrt{2}$,
联立方程得到$\left\{\begin{array}{l}{y=3-{x}^{2}}\\{y={x}^{2}-2x-1}\end{array}\right.$,解得x=-1,或x=2,
∴两曲线y=3-x2与y=x2-2x-1所围成的图形面积
S=${∫}_{-\sqrt{3}}^{\sqrt{3}}$(3-x2)dx-${∫}_{1-\sqrt{2}}^{1+\sqrt{2}}$(x2-2x-1)dx-[${∫}_{-\sqrt{3}}^{-1}$(3-x2)dx+${∫}_{-1}^{1-\sqrt{2}}$(x2-2x-1)dx]+${∫}_{\sqrt{3}}^{2}$(3-x2)dx+${∫}_{2}^{1+\sqrt{2}}$(x2-2x-1)dx=$\frac{10}{3}$+2$\sqrt{3}$-$\frac{8}{3}$+6$\sqrt{2}$+$\frac{8}{3}$-2$\sqrt{3}$+$\frac{17}{3}$-6$\sqrt{2}$=9,
故选:B.
点评 本题主要考查了学生会求出原函数的能力,以及考查了数形结合的思想,同时会利用定积分求图形面积的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {3} | C. | {1,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [1,2] | C. | [10,100] | D. | [0,lg2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 144 | B. | 480 | C. | 216 | D. | 432 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com