
【题目】(![]() )直线过点(2,3),且当倾斜角是直线
)直线过点(2,3),且当倾斜角是直线![]() 的倾斜角的二倍时,求直线方程.
的倾斜角的二倍时,求直线方程.
(![]() )当与
)当与![]() 轴正半轴交于
轴正半轴交于![]() 点、
点、![]() 轴正半轴交于
轴正半轴交于![]() 点,且
点,且![]() 的面积最小时,求直线方程.
的面积最小时,求直线方程.
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,
, ![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,平面
,平面![]() 与
与![]() 交于点
交于点![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的正切值为__________.
所成角的正切值为__________.
【答案】![]()
【解析】
延长![]() 交
交![]() 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,
由![]() ,得
,得![]() ,则
,则![]() ,所以
,所以![]() .
.
取![]() 的中点为M,连接EM,则
的中点为M,连接EM,则![]() ,
,
所以![]() ,则
,则![]() ,所以AK=
,所以AK=![]() .
.
由AD//BC,得异面直线![]() 与
与![]() 所成角即为
所成角即为![]() ,
,
则异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() .
.
【题型】填空题
【结束】
17
【题目】在极坐标系中,极点为![]() ,已知曲线
,已知曲线![]() :
: ![]() 与曲线
与曲线![]() :
: ![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)求过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一枚骰子掷一次得到2点的概率为![]() ,这说明一枚骰子掷6次会出现一次2点
,这说明一枚骰子掷6次会出现一次2点
B. 某地气象台预报说,明天本地降水的概率为70%,这说明明天本地有70%的区域下雨,30%的区域不下雨
C. 某中学高二年级有12个班,要从中选2个班参加活动,由于某种原因,一班必须参加,另外再从二至十二班中选一个班,有人提议用如下方法:掷两枚骰子得到的点数是几,就选几班,这是很公平的方法
D. 在一场乒乓球赛前,裁判一般用掷硬币猜正反面来决定谁先打球,这应该说是公平的
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)(文科)求三棱锥![]() 的体积.
的体积.
(理科)求二面角![]() 平面角正切值的大小.
平面角正切值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如表所示:
资源 消耗量 产品 | 甲产品(每吨) | 乙产品(每吨) | 资源限额(每天) |
煤( | 9 | 4 | 360 |
电力( | 4 | 5 | 200 |
劳力(个) | 3 | 10 | 300 |
利润(万元) | 7 | 12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.点E是CD边的中点,点F,G分别在线段AB,BC上,且AF=2FB,CG=2GB.

(1)证明:PE⊥FG;
(2)求二面角PADC的正切值;
(3)求直线PA与直线FG所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)=(x+l)lnx﹣ax+a (a为正实数,且为常数)
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若不等式(x﹣1)f(x)≥0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
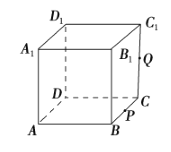
【题目】如图,正方体![]() 的棱长为 1,
的棱长为 1, ![]() 为
为![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点,过点A、P、Q的平面截该正方体所得的截面记为
上的动点,过点A、P、Q的平面截该正方体所得的截面记为![]() .则下列命题正确的是__________(写出所有正确命题的编号).
.则下列命题正确的是__________(写出所有正确命题的编号).
①当![]() 时,
时, ![]() 为四边形;②当
为四边形;②当![]() 时,
时, ![]() 为等腰梯形;③当
为等腰梯形;③当![]() 时,
时, ![]() 为六边形;④当
为六边形;④当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com