
【题目】已知数列![]() 的前n项和为
的前n项和为![]() 且
且![]() .数列
.数列![]() 为非负的等比数列,且满足
为非负的等比数列,且满足![]() ,
,![]() .
.
(Ⅰ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 的前n项和为
的前n项和为![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知公差不为零的等差数列{an}的前n项和为Sn,S3=15,a1,a4,a13成等比数列.
(1)求数列{an}的通项公式;
(2)求数列![]() 的前n项和Tn大于2020的最小自然数n.
的前n项和Tn大于2020的最小自然数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣HKLE中,底面ABCD是边长为3的正方形,对角线AC与BD相交于点O,点F在线段AH上且![]() ,BE与底面ABCD所成角为
,BE与底面ABCD所成角为![]() .
.
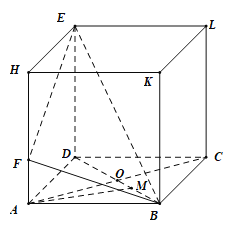
(1)求证:AC⊥BE;
(2)M为线段BD上一点,且![]() ,求异面直线AM与BF所成角的余弦值.
,求异面直线AM与BF所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F是拋物线C:y2=2px(p>0)的焦点,点M(x0,1)在C上,且|MF|=![]() .
.
(1)求p的值;
(2)若直线l经过点Q(3,-1)且与C交于A,B(异于M)两点,证明:直线AM与直线BM的斜率之积为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长轴长为![]() 的椭圆C:
的椭圆C:![]() 的左、右焦点分别为F1、F2,且以F1、F2为直径的圆与C恰有两个公共点.
的左、右焦点分别为F1、F2,且以F1、F2为直径的圆与C恰有两个公共点.
(1)求椭圆C的方程;
(2)若经过点F2的直线l与C交于M,N两点,且M,N关于原点O的对称点分别为P,Q,求四边形MNPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(cosx,sinx),
=(cosx,sinx),![]() =(cosx,﹣sinx),函数
=(cosx,﹣sinx),函数![]() .
.
(1)若![]() ,x
,x![]() (0,
(0,![]() ),求tan(x+
),求tan(x+![]() )的值;
)的值;
(2)若![]() ,
,![]() (
(![]() ,
,![]() ),
),![]() ,
,![]() (0,
(0,![]() ),求
),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com