
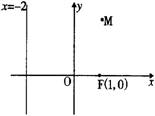
(08年宝鸡市质检二理) 在直角坐标系![]() 中,已知定点F(1,0)设平面上的动点M在直线
中,已知定点F(1,0)设平面上的动点M在直线![]() 上的射影为N,且满足
上的射影为N,且满足![]() .
.
(1)求动点M的轨迹C的方程;
(2)若直线l是上述轨迹C在点M(顶点除外)处的切线,证明直线MN与l的夹角等于直线ME与l的夹角;
(3)设MF交轨迹C于点Q,直线l交x轴于点P,求△MPQ面积的最小值.
科目:高中数学 来源: 题型:
(08年宝鸡市质检二理) 某校从4名男教师和2名女教师中任选3人参加全县教育系统举行的演讲赛。如果设随机变量ξ表示所选3人中女教师的人数.求:
(1)ξ的分布列和数学期望;
(2)“所选3人中女教师人数![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年宝鸡市质检二理) 如图:ABCD为正方形,ADPQ也是正方形,PD┴平面AC,E为PC的中点。
(1)在图中作出点E在平面BDQ上的射影![]() ,并作简单说明;
,并作简单说明;
(2)求直线AE与面BDQ所成角的余弦值。

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年宝鸡市质检二文) 已知△ABC的三个内角A、B、C成等差数列,其外接圆半径为1,且有![]() 。
。
(1)求A、B、C的大小;
(2)求△ABC的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com