
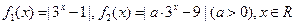 ,
, 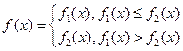 .
.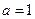 时,求
时,求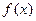 在
在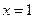 处的切线方程;
处的切线方程;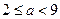 时,设
时,设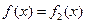 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为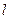 (闭区间
(闭区间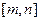 的长度定义为
的长度定义为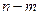 ),试求
),试求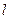 的最大值;
的最大值;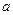 ,使得当
,使得当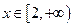 时,
时,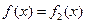 ?若存在,求出
?若存在,求出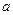 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.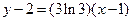 ,
,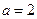 时,
时,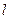 取得最大值为
取得最大值为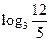
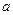 存在,且
存在,且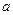 的取值范围是
的取值范围是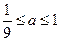
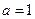 时,
时,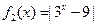 .
.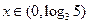 时,
时,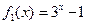 ,
,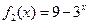 ,
,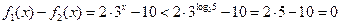 ,
,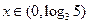 时,
时,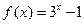 ,且
,且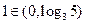 …………………………(3分)
…………………………(3分)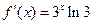 ,所以
,所以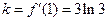 ,又
,又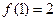 ,
,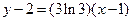 ,
,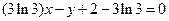 ………………………………………………………(5分)
………………………………………………………(5分)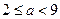 ,所以
,所以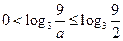 ,则
,则 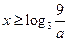 时,因为
时,因为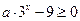 ,
,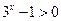 ,
,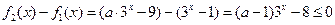 ,解得
,解得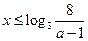 ,
,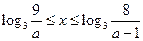 时,
时,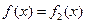 …………………………………(6分)
…………………………………(6分)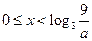 时,因为
时,因为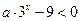 ,
,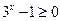 ,
,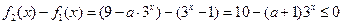 ,解得
,解得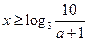 ,
,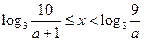 时,
时,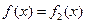 ……………………………(7分)
……………………………(7分)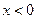 时,因为
时,因为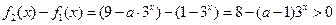 ,
,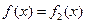 一定不成立………………………………………………………(8分)
一定不成立………………………………………………………(8分)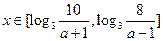 时,
时,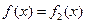 ,
,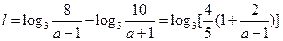 …………………………………(9分)
…………………………………(9分)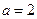 时,
时,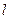 取得最大值为
取得最大值为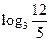 ………………………………………(10分)
………………………………………(10分)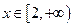 时,
时,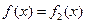 ”等价于“
”等价于“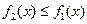 对
对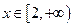 恒成立”,
恒成立”,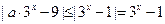 (*)对
(*)对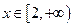 恒成立” ……………………(11分)
恒成立” ……………………(11分)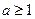 时,
时,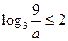 ,则当
,则当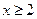 时,
时,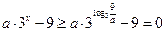 ,则(*)可化为
,则(*)可化为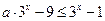 ,即
,即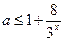 ,而当
,而当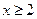 时,
时,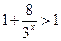 ,
,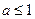 ,从而
,从而 适合题意……………………………………………………(12分)
适合题意……………………………………………………(12分)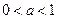 时,
时,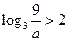 .
.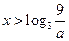 时,(*)可化为
时,(*)可化为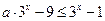 ,即
,即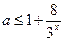 ,而
,而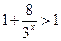 ,
,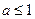 ,此时要求
,此时要求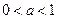 ……………………………………………(13分)
……………………………………………(13分)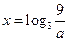 时,(*)可化为
时,(*)可化为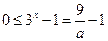 ,
,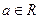 ,此时只要求
,此时只要求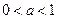 ……………………………………………(14分)
……………………………………………(14分)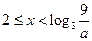 时,(*)可化为
时,(*)可化为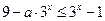 ,即
,即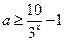 ,而
,而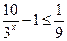 ,
,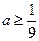 ,此时要求
,此时要求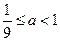 ……………………………………………(15分)
……………………………………………(15分)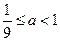 符合题意要求.
符合题意要求.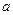 存在,且
存在,且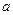 的取值范围是
的取值范围是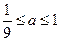 ……………………(16分)
……………………(16分)

科目:高中数学 来源:不详 题型:解答题
 的厂房(不管墙高),工程的造价是:
的厂房(不管墙高),工程的造价是:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的正方形
的正方形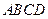
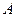 为圆心作半径为
为圆心作半径为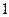 的圆弧与正方形交于
的圆弧与正方形交于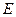 、
、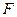 两点,在
两点,在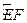 上有一动点
上有一动点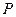 ,过
,过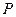 作
作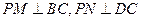 ,求矩形
,求矩形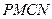 面积的最小值;
面积的最小值;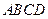 的基础上再拼接两个完全相同的正方形,求
的基础上再拼接两个完全相同的正方形,求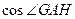 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com