已知数列{an}满足an=an+1+4,a18+a20=12,等比数列{bn}的首项为2,公比为q.
(Ⅰ)若q=3,问b3等于数列{an}中的第几项?
(Ⅱ)数列{an}和{bn}的前n项和分别记为Sn和Tn,Sn的最大值为M,当q=2时,试比较M与T9的大小.
【答案】
分析:(I)根据等比数列的性质求出b
3,然后由a
n=a
n+1+4,可知{a
n}是公差d=-4的等差数列,根据a
18+a
20=12,求出数列的首项和公差,从而求出数列的通项,令a
n=b
3求出n的值,从而得到所求;
(II)根据等比数列的求和公式求出T
9,然后根据等差数列的求和公式求出S
n,根据二次函数的性质求出S
n的最大值M,从而得到M与T
9的大小.
解答:解:(I)b
3=b
1q
2=18. …(2分)
由a
n=a
n+1+4,得a
n+1-a
n=-4,即{a
n}是公差d=-4的等差数列.…(3分)
由a
18+a
20=12,得a
1+18d=6⇒a
1=78
∴a
n=78+(n-1)(-4)=-4n+82
令-4n+82=b
3=18,得n=16
∴b
3等于数列{a
n}中的第16项
(II)∵b
1=q=2
∴T
9=

=2
10-2=1022
又S
n=78n+
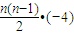
=-2n
2+80n=-2(n-20)
2+800
∴n=20时,最大值M=800
∴M<T
9点评:本小题主要考查等差数列、等比数列等基础知识,考查运算求解能力,考查化归与转化思想,属于中档题.

 =210-2=1022
=210-2=1022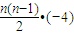 =-2n2+80n=-2(n-20)2+800
=-2n2+80n=-2(n-20)2+800

 阅读快车系列答案
阅读快车系列答案