
【题目】某公司结合公司的实际情况针对调休安排展开问卷调查,提出了![]() ,
,![]() ,
,![]() 三种放假方案,调查结果如下:
三种放假方案,调查结果如下:
支持 | 支持 | 支持 | |
35岁以下 | 20 | 40 | 80 |
35岁以上(含35岁) | 10 | 10 | 40 |
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从“支持
个人,已知从“支持![]() 方案”的人中抽取了6人,求
方案”的人中抽取了6人,求![]() 的值;
的值;
(2)在“支持![]() 方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
科目:高中数学 来源: 题型:
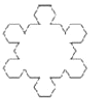
【题目】如图,第1个图形由正三角形扩展而成,共12个顶点.第n个图形是由正n+2边形扩展而来 ![]() ,则第n+1个图形的顶点个数是 ( )
,则第n+1个图形的顶点个数是 ( )
 (1)
(1)  (2)
(2) (3)
(3)  (4)
(4)
A. (2n+1)(2n+2)B. 3(2n+2)C. (n+2)(n+3)D. (n+3)(n+4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C:ρ=2sinθ,A、B为曲线C的两点,以极点为原点,极轴为x轴非负半轴的直角坐标中,曲线E:![]() 是参数)上一点P,则∠APB的最大值为 ( )
是参数)上一点P,则∠APB的最大值为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
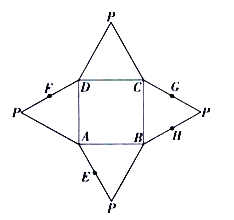
【题目】如图是一几何体的平面展开图,其中四边形![]() 为正方形,
为正方形,![]() 分别为
分别为![]() 的中点.在此几何体中,给出下列结论,其中正确的结论是( )
的中点.在此几何体中,给出下列结论,其中正确的结论是( )
A.平面![]() 平面
平面![]() B.直线
B.直线![]() 平面
平面![]()
C.直线![]() 平面
平面![]() D.直线
D.直线![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知在四棱锥![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.
的中点.
(1)判断并说明![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不
的值;若不
存在,请说明理由;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,动点
,动点![]() 异于原点
异于原点![]() 在y轴上运动,连接FP,过点P作PM交x轴于点M,并延长MP到点N,且
在y轴上运动,连接FP,过点P作PM交x轴于点M,并延长MP到点N,且![]() ,
,![]() .
.
![]() 求动点N的轨迹C的方程;
求动点N的轨迹C的方程;
![]() 若直线l与动点N的轨迹交于A、B两点,若
若直线l与动点N的轨迹交于A、B两点,若![]() 且
且![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ADEF与梯形ABCD所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,M为CE的中点,N为CD中点.
,M为CE的中点,N为CD中点.
![]() 求证:平面
求证:平面![]() 平面ADEF;
平面ADEF;
![]() 求证:平面
求证:平面![]() 平面BDE;
平面BDE;
![]() 求点D到平面BEC的距离.
求点D到平面BEC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
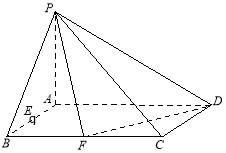
【题目】在四棱锥P-ABCD中,△PBC为正三角形,AB⊥平面PBC,AB∥CD,AB=![]() DC,
DC, ![]() .
.
(1)求证:AE∥平面PBC;
(2)求证:AE⊥平面PDC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com