
分析 首先利用正弦定理化边为角,可得2RsinAcosB-2RsinBcosA=$\frac{3}{5}$2RsinC,然后利用诱导公式、同角的三角函数的基本关系式及两角和与差的正弦公式可得tanA=4tanB,再根据两角差的正切公式、均值不等式求解即可.
解答 解:∵acosB-bcosA=$\frac{3}{5}$c,
∴2RsinAcosB-2RsinBcosA=$\frac{3}{5}$2RsinC,
∴sinAcosB-sinBcosA=$\frac{3}{5}$sinC,
∴sinAcosB-sinBcosA=$\frac{3}{5}$sin(A+B),
∴sinAcosB-sinBcosA=$\frac{3}{5}$(sinAcosB+sinBcosA),
∴2sinAcosB=8sinBcosA,
∴tanA=4tanB,
∵$\frac{π}{4}$$<B<\frac{π}{2}$,
∴tanB>1,
∴tan2B•tan3A=$\frac{2tanB}{1-{tan}^{2}B}$•tan3A=$\frac{128ta{n}^{4}B}{1-{tan}^{2}B}$,
令x=tan2B,则t>1,
y=$\frac{128{t}^{2}}{1-t}$,则y′=$\frac{128{(2-t}^{\;})}{{(1-t)}^{2}}$,
当1<t<2时,y′>0,y=$\frac{128{t}^{2}}{1-t}$为增函数,
当t>2时,y′<0,y=$\frac{128{t}^{2}}{1-t}$为减函数,
故当t=2时,y=$\frac{128{t}^{2}}{1-t}$取最大值-512,
故答案为:-512.
点评 本题考查了正弦定理、两角和与差的正弦公式、两角差的正切公式、同角的三角函数的基本关系式、均值不等式等基础知识,考查了基本运算能力,考查了转化思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
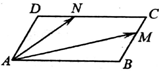 如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )
如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )| A. | [0,3] | B. | [1,4] | C. | [2,5] | D. | [1,7] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 资源 产品 | 资金(万元) | 场地(平方米) |
| A | 2 | 100 |
| B | 35 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com