
【题目】已知椭圆E: ![]() 过点
过点 ![]() ,离心率为
,离心率为 ![]() ,点F1 , F2分别为其左、右焦点.
,点F1 , F2分别为其左、右焦点.
(1)求椭圆E的标准方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点P,Q,且 ![]() ?若存在,求出该圆的方程,并求|PQ|的最大值;若不存在,请说明理由.
?若存在,求出该圆的方程,并求|PQ|的最大值;若不存在,请说明理由.
【答案】
(1)解:由题意得:e= ![]() ,a2﹣b2=c2,
,a2﹣b2=c2,
且 ![]() +
+ ![]() =1,
=1,
解得 ![]() ,a=2,b=1,
,a=2,b=1,
所以椭圆E方程为 ![]()
(2)解:假设满足条件的圆存在,其方程为:x2+y2=r2(0<r<1).
当直线PQ的斜率存在时,设直线方程为y=kx+m,
由 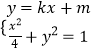 得(1+4k2)x2+8mkx+4m2﹣4=0,
得(1+4k2)x2+8mkx+4m2﹣4=0,
令P(x1,y1),Q(x2,y2),
可得 ![]() ,
, ![]() ,
,
∵ ![]() ,∴x1x2+y1y2=0
,∴x1x2+y1y2=0
∴ ![]() ,
,
∴5m2=4k2+4,
由直线PQ与圆相切,则 ![]() ,
,
所以存在圆 ![]() .
.
当直线PQ的斜率不存在时,也适合 ![]() .
.
综上所述,存在圆心在原点的圆 ![]() 满足题意.
满足题意.
由弦长公式可得: ![]()
= ![]() =
= ![]() ,
,
又 ![]() ,代入上式可得:
,代入上式可得: ![]() ,
,
令4k2+1=t,即 ![]() ,
,
则 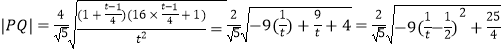 ,
,
当 ![]() 时,即
时,即 ![]() 时,
时, ![]() ,
,
当直线l的斜率k不存在时, ![]() ,
,
所以 ![]()
【解析】(1)运用椭圆的离心率公式和A在椭圆上,满足椭圆方程,解方程即可得到所求椭圆的方程;(2)假设满足条件的圆存在,其方程为:x2+y2=r2(0<r<1).当直线PQ的斜率存在时,设直线方程为y=kx+m,代入椭圆方程,运用韦达定理,由 ![]() ,可得x1x2+y1y2=0,代入化简整理,再由直线和圆相切的条件,即可得到满足条件的圆存在;运用弦长公式,化简整理,由二次函数的最值的求法,即可得到所求最大值.
,可得x1x2+y1y2=0,代入化简整理,再由直线和圆相切的条件,即可得到满足条件的圆存在;运用弦长公式,化简整理,由二次函数的最值的求法,即可得到所求最大值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下列四种说法:
①垂直于同一平面的所有向量一定共面;
②在△ABC中,已知 ![]() ,则∠A=60°;
,则∠A=60°;
③在△ABC中,sin2A=sin2B+sin2C+sinBsinC,则A= ![]()
④若a>0,b>0,a+b=2,则a2+b2≥2;
正确的序号有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞某家具生产厂家根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产书桌、书柜、电脑椅共120张,且书桌至少生产20张.已知生产这些家具每张所需工时和每张产值如表:
家具名称 | 书桌 | 书柜 | 电脑椅 |
工 时 |
|
|
|
产值(千元) | 4 | 3 | 2 |
问每周应生产书桌、书柜、电脑椅各多少张,才能使产值最高?最高产值是多少?(以千元为单位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点. 
(1)求证:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E﹣AB﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E、F为CD上两点,且EF的长为定值,则下面四个值中不是定值的是( ) 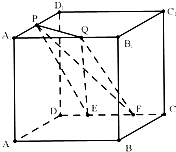
A.点P到平面QEF的距离
B.直线PQ与平面PEF所成的角
C.三棱锥P﹣QEF的体积
D.△QEF的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,点F1(﹣1,0),F2(1,0),动点M到点F2的距离是 ![]() ,线段MF1的中垂线交MF2于点P.
,线段MF1的中垂线交MF2于点P. 
(1)当点M变化时,求动点P的轨迹G的方程;
(2)设直线l:y=kx+m与轨迹G交于M、N两点,直线F2M与F2N的倾斜角分别为α、β,且α+β=π,求证:直线l经过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足:①f(x)+f(2﹣x)=0;②f(x﹣2)=f(﹣x),③在[﹣1,1]上表达式为f(x)= ![]() ,则函数f(x)与函数g(x)=
,则函数f(x)与函数g(x)= ![]() 的图象在区间[﹣3,3]上的交点个数为( )
的图象在区间[﹣3,3]上的交点个数为( )
A.5
B.6
C.7
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com