
| A. | 奇函数且在(-∞,+∞)上是增函数 | B. | 奇函数且在(-∞,+∞)上是减函数 | ||
| C. | 偶函数且在(-∞,+∞)上是增函数 | D. | 偶函数且在(-∞,+∞)上是减函数 |
分析 根据题意,由对数的运算性质可得f(x)=2x,进而可得函数F(x)的解析式,对于F(x),先分析其定义域,进而分析可得F(-x)=-F(x),即可得函数F(x)为奇函数,进而利用定义法证明可得函数为增函数,综合可得答案.
解答 解:根据题意,x-log2f(x)=0,即x=log2f(x),变形可得f(x)=2x,
函数F(x)=f(x)-$\frac{1}{f(x)}$=2x-2-x,
其定义域为R,且F(-x)=2-x-2x=-F(x),
故函数F(x)奇函数;
函数F(x)=2x-2-x=2x-$\frac{1}{{2}^{x}}$,
设x1>x2,
F(x1)-F(x2)=${2}^{{x}_{1}}$-$\frac{1}{{2}^{{x}_{1}}}$-(${2}^{{x}_{2}}$-$\frac{1}{{2}^{{x}_{2}}}$)=(${2}^{{x}_{1}}$-${2}^{{x}_{2}}$)(1+$\frac{1}{{2}^{{x}_{1}}{2}^{{x}_{2}}}$),
又由x1>x2,则${2}^{{x}_{1}}$>${2}^{{x}_{2}}$,则有${2}^{{x}_{1}}$-${2}^{{x}_{2}}$>0,
故F(x1)-F(x2)>0,
即函数F(x)为增函数;
故选:A.
点评 本题考查函数奇偶性与单调性的判断,关键是利用对数的运算性质求出f(x)和F(x)的解析式.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:选择题
| A. | 偶函数,且在(0,+∞)上是增函数 | |
| B. | 偶函数,且在(0,+∞)上是减函数 | |
| C. | 奇函数,且在(0,+∞)上是增函数 | |
| D. | 非奇非偶函数,且在(0,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -x+2y-4=0 | B. | x+2y-4=0 | C. | -x+2y+4=0 | D. | x+2y+4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2015年前三个季度中国GDP累计比较2014年同期增速有上升的趋势 | |
| B. | 相对于2014年,2015年前三个季度第三产业对GDP的贡献率明显增加 | |
| C. | 相对于2014年,2015年前三个季度第二产业对GDP的贡献率明显增加 | |
| D. | 相对于2014年,2015年前三个季度第一产业对GDP的贡献率明显增加 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (-2,0) | C. | ∅ | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
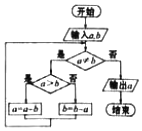 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为98,63,则输出的a为( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为98,63,则输出的a为( )| A. | 0 | B. | 7 | C. | 14 | D. | 28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com