
有下列4个命题:
①函数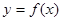 在一点的导数值为
在一点的导数值为 是函数
是函数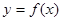 在这点取极值的充要条件;
在这点取极值的充要条件;
②若椭圆 的离心率为
的离心率为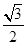 ,则它的长半轴长为1;
,则它的长半轴长为1;
③对于 上可导的任意函数
上可导的任意函数 ,若满足
,若满足 ,则必有
,则必有
④经过点(1,1)的直线,必与椭圆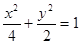 有2个不同的交点。
有2个不同的交点。
其中真命题的为 (将你认为是真命题的序号都填上)
(3)(4)
【解析】
试题分析:对于①函数 在一点的导数值为
在一点的导数值为 是函数
是函数 在这点取极值的充要条件;错误,应该是必要不充分条件。
在这点取极值的充要条件;错误,应该是必要不充分条件。
②若椭圆 的离心率为
的离心率为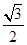 ,则它的长半轴长为1;由于焦点位置不定,应该有两个值,长半轴的长为=
,则它的长半轴长为1;由于焦点位置不定,应该有两个值,长半轴的长为= 或者1,错误。
或者1,错误。
③对于 上可导的任意函数
上可导的任意函数 ,若满足
,若满足 ,则必有
,则必有 ,利用函数单调性,当x>1,地增函数,当x<1,递减函数可知不等式成立。
,利用函数单调性,当x>1,地增函数,当x<1,递减函数可知不等式成立。
④经过点(1,1)的直线,必与椭圆 有2个不同的交点,由于点在椭圆内部,可知必然有两个交点,成立,故答案为(3)(4)
有2个不同的交点,由于点在椭圆内部,可知必然有两个交点,成立,故答案为(3)(4)
考点:导数的几何意义,以及直线与圆锥曲线
点评:主要是考查了命题真假的判定,以及极值概念和直线与圆锥曲线交点问题,属于中档题。


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com