
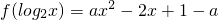 ,a∈R.
,a∈R.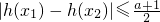 成立,求a的取值范围.
成立,求a的取值范围. >0,
>0, )上是减函数,在(
)上是减函数,在( ,+∞)上是增函数.其值域为(-
,+∞)上是增函数.其值域为(- +1-a,+∞);
+1-a,+∞); <0,
<0, log2
log2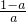 (0<a<1).
(0<a<1). log2
log2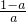 >1得0<a<
>1得0<a< ,由x0=
,由x0= log2
log2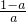 <-1,得a>
<-1,得a> ,
, (a-1),
(a-1), (a-1)>-1,得a>
(a-1)>-1,得a> .
. 时,h′(x)=aln2•2x-(1-a)lna•2-x<0恒成立,函数h(x)在[-1,1]上是减函数,
时,h′(x)=aln2•2x-(1-a)lna•2-x<0恒成立,函数h(x)在[-1,1]上是减函数, a,最小值是h(1)=
a,最小值是h(1)= (a-1).
(a-1).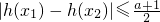 成立,
成立, a-
a- (a-1)≤
(a-1)≤ ,∴a≥2.不合,舍去.
,∴a≥2.不合,舍去. <a≤
<a≤ 时,函数h(x)在[-1,x0]上是减函数,在(x0,1]上是增函数
时,函数h(x)在[-1,x0]上是减函数,在(x0,1]上是增函数 a,最小值是h(x0)=2
a,最小值是h(x0)=2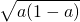 -2.
-2.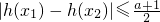 成立,
成立, a-2
a-2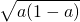 +2≤
+2≤ ,
, ≥a≥
≥a≥ .
. <a≤
<a≤ 时,函数h(x)在[-1,x0]上是减函数,在(x0,1]上是增函数
时,函数h(x)在[-1,x0]上是减函数,在(x0,1]上是增函数 (a-1),最小值是h(x0)=2
(a-1),最小值是h(x0)=2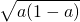 -2.
-2.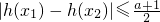 成立,
成立, (a-1)-2
(a-1)-2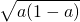 +2≤
+2≤ ,
, <a≤
<a≤ .
. 时,h′(x)=aln2•2x-(1-a)lna•2-x>0恒成立,函数h(x)在[-1,1]上是增函数,
时,h′(x)=aln2•2x-(1-a)lna•2-x>0恒成立,函数h(x)在[-1,1]上是增函数,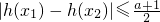 成立,
成立, (a-1)+
(a-1)+ a≤
a≤ ,
, .不合,舍去.
.不合,舍去. ,
, ].
]. 恒成立,等价于h(x)在[-1,1]内满足其最大值与最小值的差小于等于
恒成立,等价于h(x)在[-1,1]内满足其最大值与最小值的差小于等于 .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源:2012-2013学年江苏省扬州市高一(上)期末数学试卷(解析版) 题型:解答题
 ,a∈R.
,a∈R.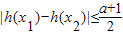 成立,求a的取值范围.
成立,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省扬州中学高一(上)期末数学试卷(解析版) 题型:解答题
 ,a∈R.
,a∈R.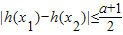 成立,求a的取值范围.
成立,求a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com