
【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 且
且![]() ,
,![]() .
.
(i)求实数![]() 的最大值;
的最大值;
(ii)证明不等式:![]() .
.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ;(ii)证明见解析.
;(ii)证明见解析.
【解析】
试题分析:(1)先求出导函数,再根据![]() ,
,![]()
![]() 由点斜式可得曲线
由点斜式可得曲线![]() 在点
在点![]() 处的切线方程;(2)(i)
处的切线方程;(2)(i)![]() 等价于
等价于![]() ,讨论
,讨论![]() 时、当
时、当![]() 时两种情况,排除不合题意的
时两种情况,排除不合题意的![]() 的值,即可得实数
的值,即可得实数![]() 的最大值,(ii)当
的最大值,(ii)当![]() 时整理得
时整理得![]() ,令
,令![]() ,则
,则![]() ,进而可证原不等式.
,进而可证原不等式.
试题解析:(1)由题意![]() 且
且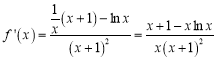 ,
,
∴![]() ,
,
又![]()
![]() ,
,
∴![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() 即
即![]()
(2)(i)由题意知![]() ,
,
设![]() ,
,
则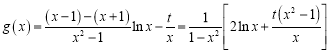 ,
,
设![]() ,
,
则![]() ,
,
(1)当![]() 时,∵
时,∵![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
∴![]() 时,
时,![]() ,又
,又![]() ,
,
∴![]() ,不符合题意.
,不符合题意.
(2)当![]() 时,设
时,设![]() ,
,
①若![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 在
在![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上单调递减又
上单调递减又![]() ,
,
∴![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
![]() 时,
时,![]() ,
,![]() ,
,![]() ,符合题意.
,符合题意.
②若![]() ,即
,即![]() 时,
时,![]() 的对称轴
的对称轴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
而![]() ,∴
,∴![]() ,不符合题意,
,不符合题意,
综上所述![]() .
.
(ii)由(i)知![]() 时,
时,![]() ,
,
当![]() 时整理得
时整理得![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]()


科目:高中数学 来源: 题型:
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:

(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附:  ,
, ![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
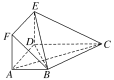
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】否定“自然数![]() 、
、![]() 、
、![]() 中恰有一个偶数”时正确的反设为( )
中恰有一个偶数”时正确的反设为( )
A. ![]() 、
、![]() 、
、![]() 都是奇数 B.
都是奇数 B. ![]() 、
、![]() 、
、![]() 至少有两个偶数
至少有两个偶数
C. ![]() 、
、![]() 、
、![]() 都是偶数 D.
都是偶数 D. ![]() 、
、![]() 、
、![]() 中都是奇数或至少有两个偶数
中都是奇数或至少有两个偶数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解2017届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为![]() .
.
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附: 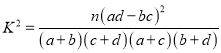
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为![]() 的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
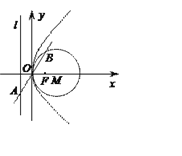
(1)求⊙M和抛物线C的方程;
(2)若P为抛物线C上的动点,求![]() 的最小值;
的最小值;
(3)过l上的动点Q向⊙M作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com