
(本小题满分10分)
如图,在四棱锥P – ABCD中,底面ABCD是边长为1的正方形,PA^底面ABCD,点M是棱PC的中点,AM^平面PBD.
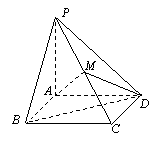 ⑴求PA的长;
⑴求PA的长;
⑵求棱PC与平面AMD所成角的正弦值.
解 如图,以A为坐标原点,AB,AD,AP分别为x,y,z轴建立空间直角坐标系,则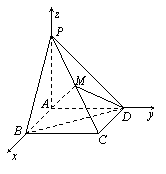 A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,a).
A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,a).
因为M是PC中点,所以M点的坐标为(,,),所以 = (,,), = (–1,1,0), = ( – 1,0,a).
⑴因为^平面PBD,所以· = · = 0.即
– + = 0,所以a = 1,即PA = 1. ………………………………………4分
⑵由 = (0,1,0), = (,,),可求得平面AMD的一个法向量n = ( – 1,0,1).又 = ( – 1,–1,1).所以cos<n, > = = = .
所以,PC与平面AMD所成角的正弦值为.……………………………10分


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com