
已知数列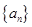 的前
的前 项和为
项和为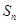 ,且
,且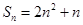 ,
,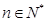 ,数列
,数列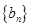 满足
满足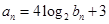 ,
,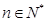 .
.
(1)求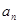 ,
,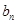 ;
;
(2)求数列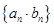 的前
的前 项和
项和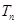 .
.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源:2011届福建省龙岩市高三上学期期末考试数学理卷(非一级校) 题型:解答题
(本题满分13分)
已知数列 的前
的前 项和为
项和为 ,满足
,满足 .
.
(Ⅰ)证明:数列 为等比数列,并
为等比数列,并 求出
求出 ;
;
(Ⅱ)设 ,求
,求 的最大项.
的最大项.
查看答案和解析>>
科目:高中数学 来源:2011年四川省泸县二中高2013届春期重点班第一学月考试数学试题 题型:解答题
(本小题14分)已知数列{ }的前
}的前 项和为
项和为 ,且
,且 =
= (
( );
); =3
=3
且 (
( ),
),
(1)写出


 ;
;
(2)求数列{ },{
},{ }的通项公式
}的通项公式 和
和 ;
;
(3)设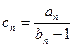 ,求数列
,求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高一下学期期中数学试卷(解析版) 题型:解答题
已知数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令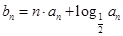 ,数列
,数列 的前
的前 项和为
项和为 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com