
【题目】如图,三棱柱![]() 的所有棱长都是
的所有棱长都是![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.

(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )求点
)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() ;(3)1
;(3)1
【解析】试题分析:(1)根据三角形相似得![]() ,根据直棱柱性质得
,根据直棱柱性质得![]() ,又由等边三角形性质得
,又由等边三角形性质得![]() ,所以由线面垂直判定定理得
,所以由线面垂直判定定理得![]() 平面
平面![]() ,即
,即![]() ,最后根据线面垂直判定定理得结论(2)建立空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,再根据向量数量积求夹角,最后根据二面角与向量夹角关系求二面角
,最后根据线面垂直判定定理得结论(2)建立空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,再根据向量数量积求夹角,最后根据二面角与向量夹角关系求二面角![]() 的余弦值.(3)根据向量投影得点
的余弦值.(3)根据向量投影得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,再利用向量数量积求夹角可得结果
,再利用向量数量积求夹角可得结果
试题解析:(![]() )证明:∵
)证明:∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() 是等边三角形,∴
是等边三角形,∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,
,
以![]() 为原点建立空间直角坐标系如图所示:
为原点建立空间直角坐标系如图所示:

则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() .
.
(![]() )
)![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,∴
,∴ ,
,
令![]() 得
得![]() ,又
,又![]() 为平面
为平面![]() 的法向量,
的法向量,
∴二面角![]() 的余弦值为
的余弦值为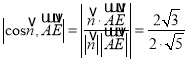
![]() .
.
(![]() )
)![]() ,
,  ,
, ![]() ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前项和为Sn , 若点An(n, ![]() )在函数f(x)=﹣x+c的图像上运动,其中c是与x无关的常数且a1=3.
)在函数f(x)=﹣x+c的图像上运动,其中c是与x无关的常数且a1=3.
(1)求数列{an}的通项公式;
(2)设bn=tanan+1tanan , tan195+tan3=atan2,求数列{bn}的前99项和(用含a的式子表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,则下列结论中正确结论的序号是__________.
,则下列结论中正确结论的序号是__________.
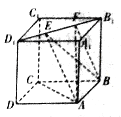
①![]() ;
;
②直线![]() 与平面
与平面![]() 所成角的正弦值为定值
所成角的正弦值为定值![]() ;
;
③当![]() 为定值,则三棱锥
为定值,则三棱锥![]() 的体积为定值;
的体积为定值;
④异面直线![]() 所成的角的余弦值为定值
所成的角的余弦值为定值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】精准扶贫是巩固温饱成果、加快脱贫致富、实现中华民族伟大“中国梦”的重要保障.某地政府在对某乡镇企业实施精准扶贫的工作中,准备投入资金将当地农产品进行二次加工后进行推广促销,预计该批产品销售量![]() 万件(生产量与销售量相等)与推广促销费
万件(生产量与销售量相等)与推广促销费![]() 万元之间的函数关系为
万元之间的函数关系为![]() (其中推广促销费不能超过5千元).已知加工此农产品还要投入成本
(其中推广促销费不能超过5千元).已知加工此农产品还要投入成本![]() 万元(不包括推广促销费用),若加工后的每件成品的销售价格定为
万元(不包括推广促销费用),若加工后的每件成品的销售价格定为![]() 元/件.
元/件.
(1)试将该批产品的利润![]() 万元表示为推广促销费
万元表示为推广促销费![]() 万元的函数;(利润=销售额-成本-推广促销费)
万元的函数;(利润=销售额-成本-推广促销费)
(2)当推广促销费投入多少万元时,此批产品的利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面ABCD为菱形,且∠ABC=60°,
AB=PC=2,PA=PB= ![]() .
.
(1)求证:平面PAB⊥平面ABCD;
(2)设H是PB上的动点,求CH与平面PAB所成最大角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com