
【题目】已知正三角形ABC的边长为2,D、E、F分别是BC、CA、AB的中点.
(1)在三角形内部随机取一点P,求满足|PB|≥1且|PC|≥1的概率;
(2)在A、B、C、D、E、F这6点中任选3点,记这3点围成图形的面积为ξ,求随机变量ξ的分布列与数学期望Eξ.
【答案】
(1)解:如图1所示,
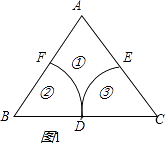
分别以正△ABC的顶点B、C为圆心,以1为半径画圆弧,交边AB、BC、AC于点F、D、E;
则点P在区域①时满足条件|PB|≥1且|PC|≥1,
其概率为P=1﹣ ![]() =1﹣
=1﹣ 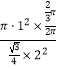 =1﹣
=1﹣ ![]()
(2)解:在A、B、C、D、E、F这6点中任选3点,共有20种不同的取法;
记这3点围成图形的面积为ξ,则ξ=0, ![]() S△,
S△, ![]() S△,S△;其中S△=
S△,S△;其中S△= ![]() ;
;
P(ξ=0)= ![]() ,P(ξ=
,P(ξ= ![]() S△)=
S△)= ![]() =
= ![]() ,P(ξ=
,P(ξ= ![]() S△)=
S△)= ![]() =
= ![]() ,P(ξ=S△)=
,P(ξ=S△)= ![]() ;
;
所以随机变量ξ的分布列为:
ξ | 0 |
|
|
|
P |
|
|
|
|
数学期望Eξ=0× ![]() +
+ ![]() ×
× ![]() +
+ ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]()
【解析】(1)根据几何概型的计算公式,求出满足条件|PB|≥1且|PC|≥1的概率值即可;(2)根据题意,求出3点围成图形的面积ξ的可能取值以及对应的概率值,列出ξ的分布列,计算数学期望Eξ的值.
【考点精析】根据题目的已知条件,利用几何概型和离散型随机变量及其分布列的相关知识可以得到问题的答案,需要掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex﹣ax,a是常数.
(Ⅰ)若a=1,且曲线y=f(x)的切线l经过坐标原点(0,0),求该切线的方程;
(Ⅱ)讨论f(x)的零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为1的动圆与定圆(x-5)2+(y+7)2=16相切,则动圆圆心的轨迹方程是( )
A. (x-5)2+(y+7)2=25
B. (x-5)2+(y+7)2=3或(x-5)2+(y+7)2=15
C. (x-5)2+(y+7)2=9
D. (x-5)2+(y+7)2=25或(x-5)2+(y+7)2=9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电力公司为了制定节电方案,需要了解居民用电情况.通过随机抽样,电力公司获得了50户居民的月平均用电量,分为六组制出频率分布表和频率分布直方图(如图所示).


(1)求a,b的值;
(2)为了解用电量较大的用户用电情况,在第5、6两组用分层抽样的方法选取5户 .
①求第5、6两组各取多少户?
②若再从这5户中随机选出2户进行入户了解用电情况,求这2户中至少有一户月平均用电量在[1000,1200]范围内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°. 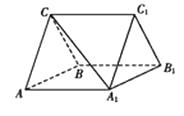
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C= ![]() ,求二面角B﹣AC﹣A1的余弦值.
,求二面角B﹣AC﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上动点M到直线x=﹣1的距离比它到点F(2,0)的距离少1.
(1)求动点M的轨迹E的方程;
(2)已知点B(﹣1,0),设过点(1,0)的直线l与轨迹E交于不同的两点P、Q,证明:x轴是∠PBQ的角平分线所在的直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,AD=PD=2,PA=2 ![]() ,∠PDC=120°,点E为线段PC的中点,点F在线段AB上.
,∠PDC=120°,点E为线段PC的中点,点F在线段AB上. 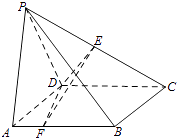
(1)若AF= ![]() ,求证:CD⊥EF;
,求证:CD⊥EF;
(2)设平面DEF与平面DPA所成二面角的平面角为θ,试确定点F的位置,使得cosθ= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com