练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （08年福州质检理）（14分）

    已知

       （1）若函数是R上的增函数，求a的取值范围；

       （2）若 的单调增区间。

    解析：（1）…………………………1分

    ∵是R上的增函数，故在R上恒成立，

    即在R上恒成立，……………………2分

    令

    …………3分

    由

    故函数上单调递减，在（－1，1）上单调递增，在（1，+）上单调递减。…………………………5分

    ∴当

    又的最小值………………6分

    ∴亦是R上的增函数。

    故知a的取值范围是……………………7分

    （2）……………………8分

    由

    ①当a=0时，上单调递增；…………10分

    可知

    ②当

    即函数在上单调递增；………………12分

    ③当时，有，

    即函数在上单调递增。………………14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年福州质检理）（12分）

    已知数列的前n项和为且对任意正整数n都有

       （1）求数列的通项公式.

       （2）设

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年福州质检理）（12分）

    已知上不相同的两个点，l是弦AB的垂直平分线.

       （1）当+取何值时，可使抛物线的焦点F与原点O到直线l的距离相等？证明你的结论；

       （2）当直线l的斜充为1时，求l在y轴上截距的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年福州质检理）（12分）

    某公司以每吨10万元的价格销售某种化工产品，每年可售出该产品1000吨，若将该产品每吨的价格上涨x%，则每年的销售数量将减少mx%，其中m为正常数.

       （1）当时，该产品每吨的价格上涨百分之几，可使销售的总金额最大？

       （2）如果涨价能使销售总金额增加，求m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

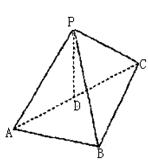
    （08年福州质检理）（12分）

    如图，P―ABC中，D是AC的中点，PA=PB=PC=

       （1）求证：PD⊥平面ABC；

       （2）求二面角P―AB―C的大小；

       （3）求AB的中点E到平面PBC的距离.

     

    查看答案和解析>>

    同步练习册答案