
【题目】已知函数f(x)=ax+x2,g(x)=xlna,a>1.
(1)求证:函数F(x)=f(x)-g(x)在(0,+∞)上单调递增;
(2)若函数y=![]() -3有四个零点,求b的取值范围;
-3有四个零点,求b的取值范围;
(3)若对于任意的x1,x2∈[-1,1]时,都有|F(x2)-F(x1)|≤e2-2恒成立,求a的取值范围.
【答案】(1)见解析(2)(2-![]() ,0)∪(2+
,0)∪(2+![]() ,+∞)(3)(1,e2]
,+∞)(3)(1,e2]
【解析】
(1)∵F(x)=f(x)-g(x)=ax+x2-xlna,
∴F′(x)=ax·lna+2x-lna=(ax-1)lna+2x.
∵a>1,x>0,∴ax-1>0,lna>0,2x>0,
∴当x∈(0,+∞)时,F′(x)>0,即函数F(x)在区间(0,+∞)上单调递增.
(2)由(1)知当x∈(-∞,0)时,F′(x)<0,
∴F(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.
∴F(x)的最小值为F(0)=1.由![]() -3=0,
-3=0,
得F(x)=b-![]() +3或F(x)=b-
+3或F(x)=b-![]() -3,
-3,
∴要使函数y=![]() -3有四个零点,只需
-3有四个零点,只需
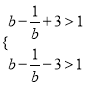 即b-
即b-![]() >4,即
>4,即![]() >0,
>0,
解得b>2+![]() 或2-
或2-![]() <b<0.
<b<0.
故b的取值范围是(2-![]() ,0)∪(2+
,0)∪(2+![]() ,+∞).
,+∞).
(3)∵x1,x2∈[-1,1],由(1)知F(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴F(x)min=F(0)=1.
从而再来比较F(-1)与F(1)的大小即可.
F(-1)=![]() +1+lna
+1+lna
∴F(1)-F(-1)=a-![]() -2lna.
-2lna.
令H(x)=x-![]() -2lnx(x>0),
-2lnx(x>0),
则H′(x)=1+![]() -
-![]() =
=![]() =
=![]() >0,
>0,
∴H(x)在(0,+∞)上单调递增.
∵a>1,∴H(a)>H(1)=0.∴F(1)>F(-1).
∴|F(x2)-F(x1)|的最大值为|F(1)-F(0)|=a-lna,
∴要使|F(x2)-F(x1)|≤e2-2恒成立,只需a-lna≤e2-2即可.令h(a)=a-lna(a>1),h′(a)=1-![]() >0,∴h(a)在(1,+∞)上单调递增.∵h(e2)=e2-2,∴只需h(a)≤h(e2),即1<a≤e2.故a的取值范围是(1,e2]
>0,∴h(a)在(1,+∞)上单调递增.∵h(e2)=e2-2,∴只需h(a)≤h(e2),即1<a≤e2.故a的取值范围是(1,e2]


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,其中
,其中![]() .若
.若![]() 对一切
对一切![]() 恒成立,则①
恒成立,则①![]() ;②
;②![]() ;③
;③![]() 既不是奇函数也不是偶函数;④
既不是奇函数也不是偶函数;④![]() 的单调递增区间是
的单调递增区间是![]() ;⑤存在经过点
;⑤存在经过点![]() 的直线与函数
的直线与函数![]() 的图像不相交.以上结论正确的是________________.(写出所有正确结论的序号)
的图像不相交.以上结论正确的是________________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
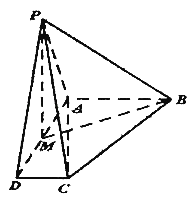
【题目】四棱锥P﹣ABCD中平面PAD⊥平面ABCD,AB∥CD,AB⊥AD,M为AD中点,PA=PD![]() ,AD=AB=2CD=2.
,AD=AB=2CD=2.
(1)求证:平面PMB⊥平面PAC;
(2)求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,椭圆
,椭圆![]() 以
以![]() 的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆
的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆![]() 、
、![]() 上,若
上,若![]() ,则直线AB的斜率k为( ).
,则直线AB的斜率k为( ).
A.1B.-1C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 满足约束条件
满足约束条件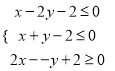 ,若
,若![]() 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数![]() 的值为__________.
的值为__________.
【答案】![]() 或
或![]()
【解析】由题可知若![]() 取得最大值的最优解不唯一则
取得最大值的最优解不唯一则![]() 必平行于可行域的某一边界,如图:
必平行于可行域的某一边界,如图: 要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
点睛:线性规划为常考题型,解决此题务必要理解最优解个数为无数个时的条件是什么,然后根据几何关系求解即可
【题型】填空题
【结束】
16
【题目】《数书九章》三斜求积术:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约一,为实,一为从隅,开平方得积”.秦九韶把三角形的三条边分别称为小斜、中斜和大斜,“术”即方法.以![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别表示三角形的面积,大斜,中斜,小斜;
分别表示三角形的面积,大斜,中斜,小斜; ![]() ,
, ![]() ,
, ![]() 分别为对应的大斜,中斜,小斜上的高;则
分别为对应的大斜,中斜,小斜上的高;则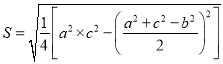
![]()
![]() .若在
.若在![]() 中
中![]() ,
, ![]() ,
, ![]() ,根据上述公式,可以推出该三角形外接圆的半径为__________.
,根据上述公式,可以推出该三角形外接圆的半径为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为:
中,曲线C的参数方程为: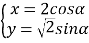 (
(![]() 为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(Ⅰ)求曲线C的普通方程和直线l的直角坐标方程;
(Ⅱ)设点P的直角坐标为![]() ,若直线l与曲线C分别相交于A,B两点,求
,若直线l与曲线C分别相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某健康社团为调查居民的运动情况,统计了某小区100名居民平均每天的运动时长(单位:小时)并根据统计数据分为![]() 六个小组(所调查的居民平均每天运动时长均在
六个小组(所调查的居民平均每天运动时长均在![]() 内),得到的频率分布直方图如图所示.
内),得到的频率分布直方图如图所示.
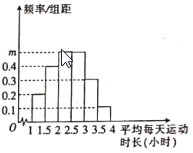
(1)求出图中![]() 的值,并估计这
的值,并估计这![]() 名居民平均每天运动时长的平均值及中位数(同一组中的每个数据可用该组区间的中点值代替);
名居民平均每天运动时长的平均值及中位数(同一组中的每个数据可用该组区间的中点值代替);
(2)为了分析出该小区居民平均每天的运动量与职业、年龄等的关系,该社团按小组用分层抽样的方法抽出20名居民进一步调查,试问在![]() 时间段内应抽出多少人?
时间段内应抽出多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知拋物线C:![]() 经过点
经过点![]() ,其焦点为F,M为抛物线上除了原点外的任一点,过M的直线l与x轴、y轴分别交于A,B两点.
,其焦点为F,M为抛物线上除了原点外的任一点,过M的直线l与x轴、y轴分别交于A,B两点.
![]() Ⅰ
Ⅰ![]() 求抛物线C的方程以及焦点坐标;
求抛物线C的方程以及焦点坐标;
![]() Ⅱ
Ⅱ![]() 若
若![]() 与
与![]() 的面积相等,证明直线l与抛物线C相切.
的面积相等,证明直线l与抛物线C相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com