
【题目】已知函数![]() .
.
(Ⅰ)求不等式![]() ;
;
(Ⅱ)若函数![]() 的最小值为
的最小值为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)|2x﹣1|<4,即﹣4<2x﹣1<4解不等式求得解集(2)g(x)=f(x)+f(x﹣1)=|2x﹣1|+|2(x﹣1)﹣1|=|2x﹣1|+|2x﹣3|≥|(2x﹣1)﹣(2x﹣3)|=2,
故g(x)的最小值为a=2,∵m+n=a=2(m>0,n>0),则
![]() =
=![]() 根据基本不等式即求得取值范围.
根据基本不等式即求得取值范围.
试题解析:
解:(1)不等式f(x)<4,即|2x﹣1|<4,即﹣4<2x﹣1<4,求得﹣![]() <x<
<x<![]() ,故不等式的解集为{x|﹣
,故不等式的解集为{x|﹣![]() <x<
<x<![]() }.
}.
(2)若函数g(x)=f(x)+f(x﹣1)=|2x﹣1|+|2(x﹣1)﹣1|=|2x﹣1|+|2x﹣3|≥|(2x﹣1)﹣(2x﹣3)|=2,
故g(x)的最小值为a=2, ∵m+n=a=2(m>0,n>0),则
![]() =
=![]() ≥
≥![]() +2
+2![]() =
=![]() +
+![]() ,故求
,故求![]() +
+![]() 的取值范围为[
的取值范围为[![]() +
+![]() ,+∞).
,+∞).


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】在一个不透明的箱子里装有5个完全相同的小球,球上分别标有数字1、2、3、4、5.甲先从箱子中摸出一个小球,记下球上所标数字后,将该小球放回箱子中摇匀后,乙再从该箱子中摸出一个小球.
(1)若甲、乙两人谁摸出的球上标的数字大谁就获胜(数字相同为平局),求甲获胜的概率;
(2)规定:两人摸到的球上所标数字之和小于6,则甲获胜,否则乙获胜,这样规定公平吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若椭圆![]() 上存在点
上存在点![]() 、
、![]() 关于直线
关于直线![]() 对称,求
对称,求![]() 的所有取值构成的集合
的所有取值构成的集合![]() ,并证明对于
,并证明对于![]() ,
, ![]() 的中点恒在一条定直线上.
的中点恒在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C1的参数方程为
中,曲线C1的参数方程为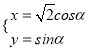 (α为参数),以原点O为极点,x轴的正半轴为级轴,建立极坐标系,曲线C2的极坐标方程
(α为参数),以原点O为极点,x轴的正半轴为级轴,建立极坐标系,曲线C2的极坐标方程![]() ;
;
(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)设P为曲线C1上的动点,求点P到曲线C2上的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列, ![]() ,
, ![]() ,
, ![]() 判断
判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,点M的坐标为![]() ,曲线C的方程为
,曲线C的方程为![]() ;以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为
;以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为![]() 的直线l经过点M.
的直线l经过点M.
(I)求直线l和曲线C的直角坐标方程:
(II)若P为曲线C上任意一点,直线l和曲线C相交于A,B两点,求△PAB面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com