
 、
、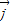 为直角坐标平面内x、y轴正方向上的单位向量,
为直角坐标平面内x、y轴正方向上的单位向量, =x
=x +(y+2)
+(y+2) ,
,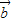 =x
=x +(y-2)
+(y-2) ,且|
,且| |+|
|+| |=8.
|=8. ,是否存在这样的直线l,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由.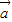 |+|
|+| |的值可推断出点M(x,y)到两个定点F1(0,-2),F2(0,2)的距离之和为8.根据椭圆的定义判断出其轨迹为椭圆,进而根据c和a,求得b,则椭圆方程可得.
|的值可推断出点M(x,y)到两个定点F1(0,-2),F2(0,2)的距离之和为8.根据椭圆的定义判断出其轨迹为椭圆,进而根据c和a,求得b,则椭圆方程可得. =
=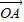 +
+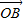 =0可推断出P与O重合,与四边形OAPB是矩形矛盾.不可知直线的斜率一定存在,设出直线方程,和A,B的坐标,把直线方程与椭圆方程联立消去y,根据韦达定理求得x1+x2和x1x2的表达式,根据
=0可推断出P与O重合,与四边形OAPB是矩形矛盾.不可知直线的斜率一定存在,设出直线方程,和A,B的坐标,把直线方程与椭圆方程联立消去y,根据韦达定理求得x1+x2和x1x2的表达式,根据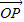 =
=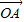 +
+ 和矩形的性质判断出OA⊥OB,即
和矩形的性质判断出OA⊥OB,即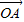 •
• =0.求得x1x2+y1y2=0,进而求得k.
=0.求得x1x2+y1y2=0,进而求得k.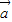 =xi+(y+2)j,
=xi+(y+2)j,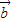 =xi+(y-2)j,且|
=xi+(y-2)j,且| |+|
|+| |=8,
|=8, =2
=2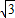
 +
+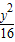 =1.
=1.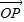 =
= +
+ =0,
=0, +
+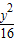 =1,消y得(4+3k2)x2+18kx-21=0.
=1,消y得(4+3k2)x2+18kx-21=0. ,x1x2=-
,x1x2=- .
.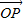 =
=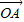 +
+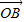 ,
,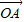 •
• =0.
=0. =(x1,y1),
=(x1,y1), =(x2,y2),
=(x2,y2), •
• =x1x2+y1y2=0,
=x1x2+y1y2=0, )+3k•(-
)+3k•(-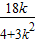 )+9=0,即k2=
)+9=0,即k2= ,得k=±
,得k=± .
. x+3,使得四边形OAPB是矩形.
x+3,使得四边形OAPB是矩形.

科目:高中数学 来源: 题型:
| 3+4i |
| x+yi |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
查看答案和解析>>
科目:高中数学 来源:江西省玉山一中2012届高三上学期期末联考数学文科试题 题型:044
设x,y∈R,![]() ,
,![]() 为直角坐标系平面内x轴、y轴正方向上的单位向量,若向量
为直角坐标系平面内x轴、y轴正方向上的单位向量,若向量![]() =x
=x![]() +(y+
+(y+![]() )
)![]() ,
,![]() =x
=x![]() +(y-
+(y-![]() )
)![]() ,且|
,且|![]() |+|
|+|![]() |=4.
|=4.
(1)求点M(x,y)的轨迹C的方程;
(2)若轨迹C上在第一角限的一点P的横坐标为1,斜率为![]() 的直线l与轨迹C交于不同两点A、B,求△PAB面积的最大值.
的直线l与轨迹C交于不同两点A、B,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年云南省、楚雄一中、昆明三中高三第二次联考理科数学 题型:解答题
((本小题满分12分)设x,y∈R,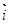 ,
,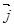 为直角坐标平面内x,y轴正方向上单位向量,若
为直角坐标平面内x,y轴正方向上单位向量,若
向量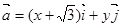 ,
,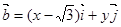 ,且
,且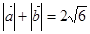 .
.
(1)求点M(x,y)的轨迹C的方程;
(2)若直线L与曲线C交于A、B两点,若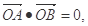 求证直线L与某个定圆E相切,并求出定圆E的方程。
求证直线L与某个定圆E相切,并求出定圆E的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
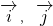 、为直角坐标系内x、y轴正方向上的单位向量,若
、为直角坐标系内x、y轴正方向上的单位向量,若 =x
=x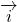 +(y+2)
+(y+2)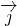 ,
, =x
=x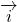 +(y-2)
+(y-2)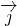 且
且 2+
2+ 2=16.
2=16.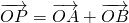 ,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.
,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省南阳一中高三(上)数学试卷1(文科)(解析版) 题型:解答题
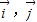 、为直角坐标系内x、y轴正方向上的单位向量,若
、为直角坐标系内x、y轴正方向上的单位向量,若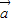 =x
=x +(y+2)
+(y+2) ,
,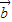 =x
=x +(y-2)
+(y-2)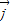 且
且 2+
2+ 2=16.
2=16.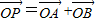 ,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.
,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com