
分析 化简可得a≥x3-3x+3-$\frac{x}{{e}^{x}}$,令g(x)=x3-3x+3-$\frac{x}{{e}^{x}}$,从而求导g′(x)=3x2-3+$\frac{x-1}{{e}^{x}}$=(x-1)(3x+3+$\frac{1}{{e}^{x}}$),从而确定gmin(x)=g(1)=1-3+3-$\frac{1}{e}$=1-$\frac{1}{e}$;从而解得.
解答 解:∵f(x)=ex(x3-3x+3)-aex-x≤0,
∴a≥x3-3x+3-$\frac{x}{{e}^{x}}$,
令g(x)=x3-3x+3-$\frac{x}{{e}^{x}}$,
g′(x)=3x2-3+$\frac{x-1}{{e}^{x}}$
=(x-1)(3x+3+$\frac{1}{{e}^{x}}$),
故当x∈[-2,1)时,g′(x)<0,
当x∈(1,+∞)时,g′(x)>0,
故g(x)在[-2,1)上是减函数,在(1,+∞)上是增函数;
故gmin(x)=g(1)=1-3+3-$\frac{1}{e}$=1-$\frac{1}{e}$;
故答案为:1-$\frac{1}{e}$.
点评 本题考查了不等式的化简与应用,同时考查了导数的综合应用及存在性问题的应用.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
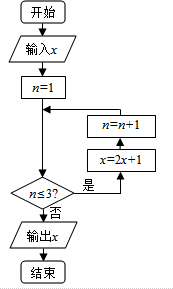 在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不在平面ABC内 | B. | D是△ABC的重心 | C. | D是△ABC的外心 | D. | D是△ABC的垂心 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com