
【题目】如图,四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,若
,若![]() ,四边形
,四边形![]() 是平行四边形,且
是平行四边形,且![]() .
.
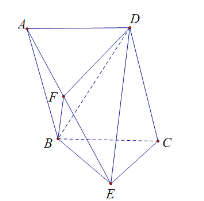
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() 平面
平面![]() ,
,![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为定义域R上的奇函数,且在R上是单调递增函数,函数
为定义域R上的奇函数,且在R上是单调递增函数,函数![]() ,数列
,数列![]() 为等差数列,且公差不为0,若
为等差数列,且公差不为0,若![]() ,则
,则![]() ( )
( )
A. 45B. 15C. 10D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1月31日晚上月全食的过程分为初亏、食既、食甚、生光、复圆五个阶段,月食的初亏发生在19时48分,20时51分食既,21时29分食甚,22时07分生光,23时11分复圆.月全食伴随有蓝月亮和红月亮,全食阶段的“红月亮”在食既时刻开始,生光时刻结束.小明准备在19:55至21:56之间的某个时刻欣赏月全食,则他等待“红月亮”的时间不超过30分钟的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 交于点
交于点![]() ,曲线
,曲线![]() 与
与![]() 轴交于点
轴交于点![]() ,求线段
,求线段![]() 的中点到点
的中点到点![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=3sin(﹣3x![]() )﹣2的图象向右平移
)﹣2的图象向右平移![]() 个单位长度得到函数g(x)的图象,若g(x)在区间[
个单位长度得到函数g(x)的图象,若g(x)在区间[![]() ,θ]上的最大值为1,则θ的最小值为( )
,θ]上的最大值为1,则θ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() )的焦点为
)的焦点为![]() ,
,![]() 为
为![]() 上一动点,点
上一动点,点![]() ,以线段
,以线段![]() 为直径作
为直径作![]() .当
.当![]() 过
过![]() 时,
时,![]() 的面积为3.
的面积为3.
(1)求![]() 的方程;
的方程;
(2)是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被
被![]() 所截得的弦长为定值?若存在,求
所截得的弦长为定值?若存在,求![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com