
分析 由已知,分类讨论,利用同角三角函数基本关系式可求cosα,tanα,进而利用两角差的正切函数公式即可计算求值得解.
解答 解:当α∈(0,$\frac{π}{2}$)时,由sinα=$\frac{3}{5}$,可得:cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{4}{5}$,tan$α=\frac{sinα}{cosα}$=$\frac{3}{4}$,可得:tan(α-$\frac{π}{4}$)=$\frac{tanα-1}{1+tanα}$=-$\frac{1}{7}$;
当α∈($\frac{π}{2}$,π)时,由sinα=$\frac{3}{5}$,可得:cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{4}{5}$,tan$α=\frac{sinα}{cosα}$=-$\frac{3}{4}$,可得:tan(α-$\frac{π}{4}$)=$\frac{tanα-1}{1+tanα}$=-7.
故答案为:-$\frac{1}{7}$或-7.(漏解或错解均不得分)
点评 本题主要考查三角函数恒等变换与求值问题,考查分类讨论的思想方法,属于基础题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [0,+∞) | C. | (4,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,4] | B. | [3,4] | C. | (-∞,0)∪(0,4] | D. | (-∞,-1)∪(0,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -4 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -2 | C. | -4 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
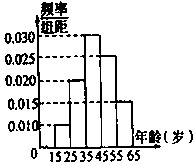 某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:| 组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的概率 |
| 第1组 | [15,25) | 5 | 0.5 |
| 第2组 | [25,35) | a | 0.9 |
| 第3组 | [35,45) | 27 | x |
| 第4组 | [45,55) | b | 0.36 |
| 第5组 | [55,65) | 3 | y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com