
分析 求出直线$\frac{x}{2}$+$\frac{y}{6}$=1的斜率,从而得到过点(-1,5),且与直线$\frac{x}{2}$+$\frac{y}{6}$=1垂直的直线方程的斜率,由此能求出所求方程.
解答 解:∵直线$\frac{x}{2}$+$\frac{y}{6}$=1的斜率k=-3,
∴过点(-1,5),且与直线$\frac{x}{2}$+$\frac{y}{6}$=1垂直的直线方程的斜率k′=$\frac{1}{3}$,
∴过点(-1,5),且与直线$\frac{x}{2}$+$\frac{y}{6}$=1垂直的直线方程为:
$y-5=\frac{1}{3}(x+1)$,
整理,得x-3y+16=0.
故答案为:x-3y+16=0.
点评 本题考查直线方程的求法,是基础题,解题时要认真审题,注意直线与直线垂直的性质的合理运用.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:解答题
 在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求:
在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 正三棱柱ABC一A1B1C1的底面边长为2,D为AB上一点,如图,建立空间直角坐标系.
正三棱柱ABC一A1B1C1的底面边长为2,D为AB上一点,如图,建立空间直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北冀州市高二文上月考三数学试卷(解析版) 题型:解答题
从一条生产线上每隔30分钟取一件产品,共取了 件,测得其产品尺寸后,画出其频率分布直方图如图,已知尺寸在
件,测得其产品尺寸后,画出其频率分布直方图如图,已知尺寸在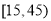 内的频数为92.
内的频数为92.

(Ⅰ)求 的值;
的值;
(Ⅱ)求尺寸在 内产品的个数;
内产品的个数;
(Ⅲ)估计尺寸大于25的频率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com