
| y-5 |
| x+3 |
| 3 |
| 4 |
| x-3 |
| 2 |
| y+5 |
| 2 |
|
|
| 8 |
| 3 |


科目:高中数学 来源: 题型:
(1)当λ为何值时,点P在一、三象限的角平分线上?
(2)当λ为何值时,点P在第三象限内?
查看答案和解析>>
科目:高中数学 来源:2010-2011年吉林省高一下学期第一次月考数学试卷 题型:解答题
(本题满分16分)
(提示:1、12、13、14班同学请完成试题(B),其他班级同学任选试题(A)或(B)作答)
(A) 已知点A(2,3),B(5,4),C(7,10)及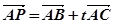 ,试问:
,试问:
(1)t为何值时,P在第三象限?
(2)是否存在D点使得四边形ABCD为平行四边形,若存在,求出D点坐标.
(B) 已知平行四边形ABCD,对角线AC与BD交于点E,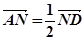 ,连接BN交AC于M,
,连接BN交AC于M,
(1)若 求实数λ.
求实数λ.
(2)若B(0,0),C(1,0),D(2,1),求M的坐标
查看答案和解析>>
科目:高中数学 来源:2010-2011年内蒙古高一第二学期期中考试理科数学 题型:解答题
附加题(共3个小题每个小题5分)
1、已知x>y>0且xy=1,  的最小值是_____________
的最小值是_____________
2、已知点A(-3,5),B(0,3)试在直线y=x+1上找一点P使|PA|+|PB|最小求出最小值是
3、数列 中,
中, ,
, ,则通项
,则通项 ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com