
【题目】如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10 ![]() 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.
海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里. 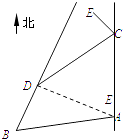
(1)求乙船每小时航行多少海里?
(2)在C的北偏西30°方向且与C相距 ![]() 海里处有一个暗礁E,周围
海里处有一个暗礁E,周围 ![]() 海里范围内为航行危险区域.问:甲、乙两船按原航向和速度航行有无危险?若有危险,则从有危险开始,经过多少小时后能脱离危险?若无危险,请说明理由.
海里范围内为航行危险区域.问:甲、乙两船按原航向和速度航行有无危险?若有危险,则从有危险开始,经过多少小时后能脱离危险?若无危险,请说明理由.
【答案】
(1)解:如图,连接AD,CD,由题意CD=10,AC= ![]() =10,∠ACD=60°
=10,∠ACD=60°
∴△ACD是等边三角形,
∴AD=10,
∵∠DAB=45°
△ABD中,BD= ![]() =10,
=10,
∴v=10×3=30海里.
答:乙船每小时航行30海里.
(2)解:建立如图所示的坐标系,危险区域在以E为圆心,r= ![]() 的圆内,直线BD的方程为y=
的圆内,直线BD的方程为y= ![]() x,∠DAB=∠DBA=45°
x,∠DAB=∠DBA=45°
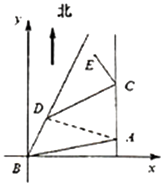
E的坐标为(ABcos15°﹣CEsin30°,ABsin15°+CEcos30°+AC),
求得A(5 ![]() +5,5
+5,5 ![]() ﹣5),C(5
﹣5),C(5 ![]() +5,5
+5,5 ![]() +5),E(5+
+5),E(5+ ![]() ,9+5
,9+5 ![]() ),
),
E到直线BD的距离d1= ![]() =1<
=1< ![]() ,故乙船有危险;
,故乙船有危险;
点E到直线AC的距离d2= ![]() >
> ![]() ,故甲船没有危险.
,故甲船没有危险.
以E为圆心,半径为 ![]() 的圆截直线BD所得的弦长分别为l=2
的圆截直线BD所得的弦长分别为l=2 ![]() =2,
=2,
乙船遭遇危险持续时间为t= ![]() =
= ![]() (小时),
(小时),
答:甲船没有危险,乙船有危险,且在遭遇危险持续时间 ![]() 小时后能脱离危险.
小时后能脱离危险.
【解析】(1)连接AD,CD,推断出△ACD是等边三角形,在△ABD中,利用余弦定理求得BD的值,进而求得乙船的速度.(2)建立如图所示的坐标系,危险区域在以E为圆心,r= ![]() 的圆内,求出E到直线BD的距离,与半径比较,即可得出结论.
的圆内,求出E到直线BD的距离,与半径比较,即可得出结论.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]()
(1)求![]() 的轨迹
的轨迹![]()
(2)过轨迹![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() ,设直线
,设直线![]() 的斜率分别是
的斜率分别是![]() ,试问在三个斜率都存在且不为0的条件下,
,试问在三个斜率都存在且不为0的条件下,  是否是定值,请说明理由,并加以证明.
是否是定值,请说明理由,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c, ![]() =(
=( ![]() ,1),
,1), ![]() =(sinA,cosA),
=(sinA,cosA), ![]() 与
与 ![]() 的夹角为60°. (Ⅰ)求角A的大小;
的夹角为60°. (Ⅰ)求角A的大小;
(Ⅱ)若sin(B﹣C)=2cosBsinC,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x+ ![]() )+cosx,x∈R,
)+cosx,x∈R,
(1)求函数f(x)的最大值,并写出当f(x)取得最大值时x的取值集合;
(2)若α∈(0, ![]() ),f(α+
),f(α+ ![]() )=
)= ![]() ,求f(2α)的值.
,求f(2α)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 有一个面是多边形,其余各面都是三角形,由这些面围成的几何体是棱锥
B. 有两个面平行且相似,其余各面都是梯形的多面体是棱台
C. 如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥可能为六棱锥
D. 有两个相邻侧面是矩形的棱柱是直棱柱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,且a3=﹣6,a6=0.
(1)求{an}的通项公式.
(2)若等比数列{bn}满足b1=8,b2=a1+a2+a3 , 求{bn}的前n项和公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点. 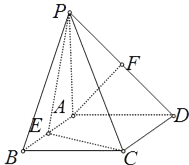
(1)求证:AF∥平面PCE;
(2)求三棱锥C﹣BEP的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com