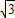Question

从一点P引三条射线PA、PB、PC且两两成60°角，则二面角A-PB-C的余弦值是    ．

Answer 1

【答案】分析：在射线PB上取一点M，过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C，连接AC在△ACM中，作AN垂直于CM于点N，∠AMN就是二面角A-PB-C的平面角，解三角形AMN，即可得到二面角A-PB-C的余弦．
解答：解：在射线PB上取一点M，过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C，连接AC 由图看出，在直角△PAM中，∠APM=60°，令PM=a，则AP=2a AM=a 同样，在直角△PCM中，∠CPM=60°，令PM=a，则CP=2a CM=a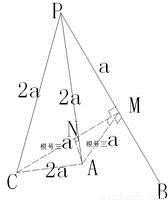 由于∠APC=60°，PA=PC=2a 所以△PAC为等边三角形，AC=2a 在△ACM中，作AN垂直于CM于点N，令MN=b，CN=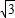a-b，AN=x，由勾股定理，△AMN中 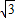（a）²-x²=b²△ACN中 （2a）²-x²=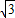（a-b）²联合两式消去x整理的，a=b 即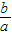=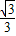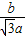，= 所以 cosM=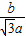=∴二面角A-PB-C的余弦值是
故答案为：
点评：本题考查的知识点是二面角的平面角及求法，其中求出二面角的平面角是解答本题的关键．