
【题目】如图,已知某几何体的三视图如下(单位:cm). 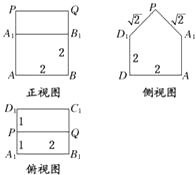
(1)画出这个几何体的直观图(不要求写画法);
(2)求这个几何体的表面积及体积.
【答案】
(1)解:这个几何体的直观图如图所示.
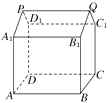
(2)解:这个几何体可看成是正方体AC1及直三棱柱B1C1Q﹣A1D1P的组合体.
由PA1=PD1= ![]() ,A1D1=AD=2,
,A1D1=AD=2,
可得PA1⊥PD1.
故所求几何体的表面积
S=5×22+2× ![]() 2×1+2×
2×1+2× ![]() ×2
×2
=22+4 ![]() (cm2),
(cm2),
所求几何体的体积V=23+ ![]() ×(
×( ![]() )2×2=10(cm3).
)2×2=10(cm3).
【解析】(1)根据三视图的画出,进行复原画出几何体的图形即可.(2)几何体可看成是正方体AC1及直三棱柱B1C1Q﹣A1D1P的组合体,求出底面面积,然后求出体积即可.
【考点精析】利用由三视图求面积、体积和空间几何体的直观图对题目进行判断即可得到答案,需要熟知求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积;立体图形的直观图要严格按照斜二测画法,在直观图中,原来与轴平行的线段仍然与轴平行,角的大小一般都会改变.


科目:高中数学 来源: 题型:
【题目】已知某产品的历史收益率的频率分布直方图如图所示.
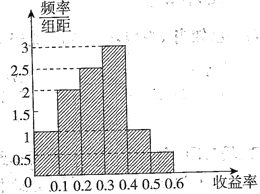
(1)试估计该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
根据表中数据算出![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从表中五组销量数据中随机抽取两组,记其中销量超过6万份的组数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当a为何值时,直线l与圆C相切;
(2)当直线l与圆C相交于A、B两点,且AB=2 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,f(x)在[0,+∞)上是增函数,且f( ![]() )=0,则不等式f(
)=0,则不等式f( ![]() )>0的解集为( )
)>0的解集为( )
A.(0, ![]() )∪(2,+∞)
)∪(2,+∞)
B.( ![]() ,1)∪(2,+∞)??
,1)∪(2,+∞)??
C.(0, ![]() )
)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位女教师的概率.
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明“1+2+22+…+2n-1=2n-1(n∈N+)”的过程中,第二步n=k时等式成立,则当n=k+1时,应得到( )
A.1+2+22+…+2k-2+2k-1=2k+1-1
B.1+2+22+…+2k+2k+1=2k-1+2k+1
C.1+2+22+…+2k-1+2k+1=2k+1-1
D.1+2+22+…+2k-1+2k=2k+1-1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数 y=f(x) 对任意的x,y∈R,满足条件:f(x+y)=f(x)+f(y)﹣2,且当x>0时,f(x)>2
(1)求f(0)的值;
(2)证明:函数f(x)是R上的单调增函数;
(3)解不等式f(2t2﹣t﹣3)﹣2<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com