
【题目】设函数![]() ,其中
,其中![]() .函数
.函数![]() 的图像在点
的图像在点![]() 处的切线与函数
处的切线与函数![]() 的图像在点
的图像在点![]() 处的切线互相垂直.
处的切线互相垂直.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)求f(x)的导函数,代入g(x),对函数g(x)求导,结合函数f(x)的图象在点A处的切线与g(x)的图象在点B处的切线互相垂直列式求t值;(Ⅱ)设函数F(x)=kg(x)﹣2f(x)=2kex(x+1)﹣2x2﹣8x﹣4,(x≥﹣2),求其导函数,分类求得函数最小值,可得k的取值范围.
(Ⅰ)由![]() 得,
得,![]() .
.
于是![]() ,所以
,所以![]() .
.
函数![]() 的图象在点
的图象在点![]() 处的切线与函数
处的切线与函数![]() 的图象在点
的图象在点![]() 处的切线互相垂直,所以
处的切线互相垂直,所以![]() ,即
,即![]()
![]()
(Ⅱ)![]() ,
,![]() .
.
设函数![]() =
=![]() (
(![]() ),
),
则![]() =
=![]() .
.
由题设可知![]() ,即
,即![]() .令
.令![]()
![]() 得
得![]()
![]() ,
,![]()
![]() .
.
(1)若![]() ,则
,则![]() ,此时
,此时![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,所以
单调递增,所以![]() 在
在![]() 取
取
最小值![]() .
.
而![]()
![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]() 恒成立.
恒成立.
②若![]() 则
则![]() ,此时
,此时![]()
![]() 在
在![]() 单调递增,而
单调递增,而![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() 恒成立.
恒成立.
③若![]() 则
则![]() ,此时
,此时![]()
![]() .
.
![]() 当
当![]() 时,
时, ![]() 不能恒成立.
不能恒成立.
综上所述,![]() 的取值范围是
的取值范围是![]()


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)离心率为
(a>b>0)离心率为![]() ,其短轴长为2.
,其短轴长为2.
(1)求椭圆C的标准方程;
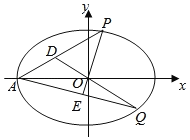
(2)如图,A为椭圆C的左顶点,P,Q为椭圆C上两动点,直线PO交AQ于E,直线QO交AP于D,直线OP与直线OQ的斜率分别为k1,k2,且k1k2=![]() ,
,![]()
![]() (λ,μ为非零实数),求λ2+μ2的值.
(λ,μ为非零实数),求λ2+μ2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为![]() .
.
![]() 求曲线C的直角坐标方程与直线l的极坐标方程;
求曲线C的直角坐标方程与直线l的极坐标方程;
![]() Ⅱ
Ⅱ![]() 若直线
若直线![]() 与曲线C交于点
与曲线C交于点![]() 不同于原点
不同于原点![]() ,与直线l交于点B,求
,与直线l交于点B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中真命题是![]()
![]()
A. 同垂直于一直线的两条直线互相平行
B. 底面各边相等,侧面都是矩形的四棱柱是正四棱柱
C. 过空间任一点与两条异面直线都垂直的直线有且只有一条
D. 过球面上任意两点的大圆有且只有一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,以
为极点,以![]() 轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆
轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆![]() 的方程为
的方程为![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量x,y满足约束条件,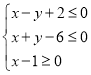
(1)画出上述不等式组所表示的平面区域;
(2)求z=2x﹣y的最大值;
(3)求z=(x+1)2+(y﹣4)2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
问:(1)由题意列出学生语文成绩与外语成绩关系的![]() 列联表:
列联表:
语文优秀 | 语文不优秀 | 总计 | |
外语优秀 | |||
外语不优秀 | |||
总计 |
(2)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?(保留三位小数)
(附: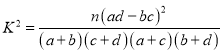 )
)
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com