已知函数f(x)=(x-a)lnx,(a≥0).
(1)当a=0时,若直线y=2x+m与函数y=f(x)的图象相切,求m的值;
(2)若f(x)在[1,2]上是单调减函数,求a的最小值;
(3)当x∈[1,2e]时,|f(x)|≤e恒成立,求实数a的取值范围.(e为自然对数的底).
【答案】
分析:(1)求导函数,利用直线y=2x+m与函数y=f(x)的图象相切,求切点坐标,即可求m的值;
(2)利用f(x)在[1,2]上是单调减函数,可得
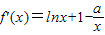
≤0在[1,2]上恒成立,分离参数,求最值,即可求得a的最小值;
(3)当x∈[1,2e]时,|f(x)|≤e恒成立,等价于-e≤(x-a)lnx≤e,|f(x)|≤e恒成立,分离参数,求最值,即可求得实数a的取值范围.
解答:解:(1)当a=0时,f(x)=xlnx,∴f′(x)=lnx+1
∵直线y=2x+m与函数y=f(x)的图象相切,∴lnx+1=2,∴x=e
∵f(e)=e,∴切点为(e,e),∴m=-e;
(2)
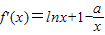
∵f(x)在[1,2]上是单调减函数,
∴
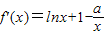
≤0在[1,2]上恒成立
∴a≥xlnx+x在[1,2]上恒成立
令g(x)=xlnx+x,则g′(x)=lnx+2>0
∴g(x)=xlnx+x在[1,2]上单调递增
∴a≥≥g(2)=2ln2+2
∴a的最小值为2ln2+2;
(3)|f(x)|≤e等价于-e≤(x-a)lnx≤e
∴-
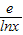
≤x-a≤
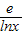
∴x-
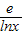
≤a≤x+

设h(x)=x+
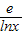
,t(x)=x-
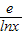
,则t(x)
max≤a≤h(x)
min,
由
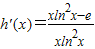
,∵h′(e)=0
令s(x)=xln
2x-e,x∈[1,2e],则s′(x)=ln
2x+lnx>0
∴h(x)在[1,2e]上单调递增,∴h(x)
min=h(e)=2e,
∵t′(x)=1+
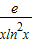
>0,∴t(x)在[1,2e]上单调递增,
∴t(x)
max=t(2e)=2e-
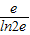
综上,2e-
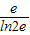
≤a≤2e.
点评:本题考查导数知识的运用,考查导数的几何意义,考查恒成立问题,分离参数求最值是关键.

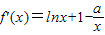 ≤0在[1,2]上恒成立,分离参数,求最值,即可求得a的最小值;
≤0在[1,2]上恒成立,分离参数,求最值,即可求得a的最小值;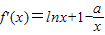
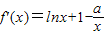 ≤0在[1,2]上恒成立
≤0在[1,2]上恒成立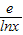 ≤x-a≤
≤x-a≤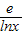
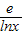 ≤a≤x+
≤a≤x+
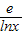 ,t(x)=x-
,t(x)=x-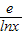 ,则t(x)max≤a≤h(x)min,
,则t(x)max≤a≤h(x)min,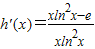 ,∵h′(e)=0
,∵h′(e)=0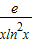 >0,∴t(x)在[1,2e]上单调递增,
>0,∴t(x)在[1,2e]上单调递增,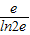
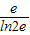 ≤a≤2e.
≤a≤2e.
