
【题目】“六艺”源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”.某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“礼”与“乐”必须排在前两节,“射”和“御”两讲座必须相邻的不同安排种数为________.
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】我国古代著名的![]() 周髀算经
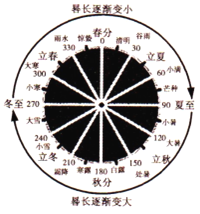
周髀算经![]() 中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷
中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷![]() 长一丈三尺五寸,夏至晷长一尺六寸
长一丈三尺五寸,夏至晷长一尺六寸![]() 意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为
意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为![]() 分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分
分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分![]() 则“立春”时日影长度为
则“立春”时日影长度为![]()
![]()
A. ![]() 分B.
分B. ![]() 分C.
分C. ![]() 分D.
分D. ![]() 分
分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列![]() 前
前![]() 项和为
项和为![]() ,且满足
,且满足![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 前
前![]() 项和
项和![]() ;
;
(3)在数列![]() 中,是否存在连续的三项
中,是否存在连续的三项![]() ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某企业生产某种产品的年固定成本为200万元,且每生产1吨该产品需另投入12万元,现假设该企业在一年内共生产该产品![]() 吨并全部销售完.每吨的销售收入为
吨并全部销售完.每吨的销售收入为![]() 万元,且
万元,且 .
.
(1)求该企业年总利润![]() (万元)关于年产量
(万元)关于年产量![]() (吨)的函数关系式;
(吨)的函数关系式;
(2)当年产量为多少吨时,该企业在这一产品的生产中所获年总利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十三届全国人大常委会第十一次会议审议的《固体废物污染环境防治法(修订草案)》中,提出推行生活垃圾分类制度,这是生活垃圾分类首次被纳入国家立法中.为了解某城市居民的垃圾分类意识与政府相关法规宣传普及的关系,对某试点社区抽取![]() 户居民进行调查,得到如下的
户居民进行调查,得到如下的![]() 列联表.
列联表.
分类意识强 | 分类意识弱 | 合计 | |
试点后 |
| ||
试点前 |
| ||
合计 |
|
已知在抽取的![]() 户居民中随机抽取
户居民中随机抽取![]() 户,抽到分类意识强的概率为
户,抽到分类意识强的概率为![]() .
.
(1)请将上面的![]() 列联表补充完整;
列联表补充完整;
(2)判断是否有![]() 的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
参考公式: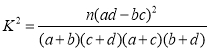 ,其中
,其中![]() .
.
下面的临界值表仅供参考
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点为
的右顶点为![]() ,
,![]() 为上顶点,点
为上顶点,点![]() 为椭圆
为椭圆![]() 上一动点.
上一动点.
(1)若![]() ,求直线
,求直线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)设![]() 为椭圆
为椭圆![]() 的右焦点,过点
的右焦点,过点![]() 与
与![]() 轴垂直的直线为
轴垂直的直线为![]() ,
,![]() 的中点为
的中点为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,求证:直线
,求证:直线![]() 与直线
与直线![]() 的交点在椭圆
的交点在椭圆![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 |
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市12月1日-20日AQI指数变化趋势:

下列叙述正确的是( )
A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占![]()
C.该市12月的前半个月的空气质量越来越好
D.总体来说,该市12月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com