
【题目】已知椭圆C:![]() 1(a>b>0),A(﹣a,0),B(0,﹣b),P为C上位于第一象限的动点,PA交y轴于点E,PB交x轴于点F.
1(a>b>0),A(﹣a,0),B(0,﹣b),P为C上位于第一象限的动点,PA交y轴于点E,PB交x轴于点F.
(1)探究四边形AEFB的面积是否为定值,说明理由;
(2)当△PEF的面积达到最大值时,求点P的坐标.
【答案】(1)面积为定值,详见解析(2)
【解析】
(1)设![]() ,写出直线方程求出
,写出直线方程求出![]() 坐标,计算面积
坐标,计算面积![]() 可得定值;
可得定值;
(2)求出![]() 到直线
到直线![]() 的距离
的距离![]() ,由(1)知
,由(1)知![]() 面积最大时,
面积最大时,![]() 面积最大,从而只要
面积最大,从而只要![]() 最大即可,
最大即可,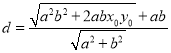 ,由
,由![]() 在椭圆上,利用基本不等式可得
在椭圆上,利用基本不等式可得![]() 的最大值,从而得出结论.
的最大值,从而得出结论.
(1)设P(x0,y0),四边形AEFB的面积为定值,证明如下:
则PA的方程为![]() ,可得
,可得 ,故
,故![]() ,
,
同理可得,![]() ,
,
从而四边形AEFB的面积为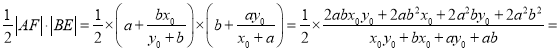 ab,
ab,
所以四边形AEFB的面积为ab.
(2)由题设知直线AB:bx+ay+ab=0,
点P到AB的距离为d,则![]() ,
,
由(1)可知,当且仅当△ABP的面积最大时,△PEF的面积最大,所以当d取最大值时,△PEF的面积最大,
由于P在C上,故![]() ,可得
,可得![]() ,
,
所以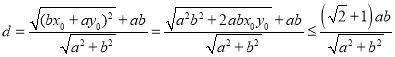 ,
,
当且仅当![]() ,即
,即![]() ,
,![]() 时等号成立,
时等号成立,
所以点P的坐标为 .
.


科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列五个命题中真命题的个数是( )
(1)若![]() 是奇函数,则
是奇函数,则![]() 的图像关于
的图像关于![]() 轴对称;
轴对称;
(2)若![]() ,则
,则![]() ;
;
(3)若函数![]() 对任意
对任意![]() 满足
满足![]() ,则8是函数
,则8是函数![]() 的一个周期;
的一个周期;
(4)命题“存在![]() ,
,![]() ”的否定是“任意
”的否定是“任意![]() ,
,![]() ”;
”;
(5)已知函数![]() ,若
,若![]() ,则
,则![]() .
.
A.2B.3C.4D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较注射![]() ,
,![]() 两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物
两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物![]() ,另一组注射药物
,另一组注射药物![]() .下表1和表2分别是注射药物
.下表1和表2分别是注射药物![]() 和药物
和药物![]() 的试验结果.(疱疹面积单位:
的试验结果.(疱疹面积单位:![]() )
)
表1:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
疱疹面积 |
|
|
|
|
频数 | 30 | 40 | 20 | 10 |
表2:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
疱疹面积 |
|
|
|
|
|
频数 | 10 | 25 | 20 | 30 | 15 |
附: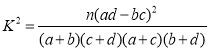
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小(不必算出中位数);
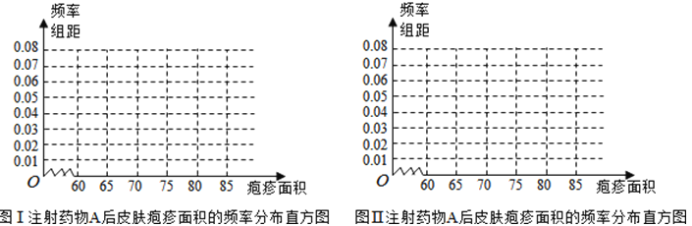
(2)完成下面![]() 列联表,并回答能否有99.9%的把握认为“注射药物
列联表,并回答能否有99.9%的把握认为“注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 后的疱疹面积有差异”.
后的疱疹面积有差异”.
表3:
疱疹面积小于 | 疱疹面积不小于 | 合计 | |
注射药物 |
|
| |
注射药物 |
|
| |
合计 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用 (基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费
元,在下一年续保时,实行的是费率浮动机制,保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费![]() 基准保费
基准保费![]() (
(![]() 浮动比率
浮动比率![]() ).发生交通事故的次数越多,出险次数的就越多,费率也就越髙,具体浮动情况如下表:
).发生交通事故的次数越多,出险次数的就越多,费率也就越髙,具体浮动情况如下表:

某机构为了研究某一品牌普通6座以下私家车的投保情况,为此搜集并整理了100辆这一品牌普通6座以下私家车一年内的出险次数,得到下面的柱状图:

已知小明家里有一辆该品牌普通6座以下私家车且需要续保,续保费用为![]() 元.
元.
(1)记![]() 为事件“
为事件“![]() ”,求
”,求![]() 的估计值;
的估计值;
(2)求![]() 的平均估计值.
的平均估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 为等边三角形,边长为2,
为等边三角形,边长为2,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面ABCD.
平面ABCD.
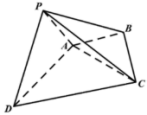
(1)证明:![]() 平面PAD;
平面PAD;
(2)求平面PAD与平面PBC所成锐二面角的余弦值;
(3)棱PD上是否存在一点E,使得![]() 平面PBC?若存在,求出
平面PBC?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com