
【题目】函数y=f(x)导函数的图象如图所示,则下列说法错误的是( )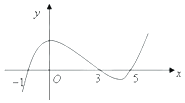
A.(﹣1,3)为函数y=f(x)的递增区间
B.(3,5)为函数y=f(x)的递减区间
C.函数y=f(x)在x=0处取得极大值
D.函数y=f(x)在x=5处取得极小值
科目:高中数学 来源: 题型:
【题目】已知函数y=f(2x+1)定义域是[﹣1,0],则y=f(x+1)的定义域是( )
A.[﹣1,1]
B.[0,2]
C.[﹣2,0]
D.[﹣2,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 在点(1,f(1))处的切线方程为x+y=2. (Ⅰ)求a,b的值;
在点(1,f(1))处的切线方程为x+y=2. (Ⅰ)求a,b的值;
(Ⅱ)若对函数f(x)定义域内的任一个实数x,都有xf(x)<m恒成立,求实数m的取值范围.
(Ⅲ) 求证:对一切x∈(0,+∞),都有3﹣(x+1)f(x)> ![]() ﹣
﹣ ![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )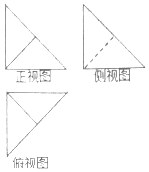
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,(e为自然对数的底数,a,b∈R),若f(x)在x=0处取得极值,且x﹣ey=0是曲线y=f(x)的切线.
,(e为自然对数的底数,a,b∈R),若f(x)在x=0处取得极值,且x﹣ey=0是曲线y=f(x)的切线.
(1)求a,b的值;
(2)用min{m,n}表示m,n中的最小值,设函数 ![]() ,若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
,若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为 ![]() (θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(Ⅰ)求C1和C2在直角坐标系下的普通方程;
(Ⅱ)已知直线l:y=x和曲线C1交于M,N两点,求弦MN中点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月1日起全国统一实施全面的两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取70后80后作为调查对象,随机调查了100人并对调查结果进行统计,70后不打算生二胎的占全部调查人数的15%,80后打算生二胎的占全部被调查人数的45%,100人中共有75人打算生二胎.
(1)根据调查数据,判断是否有90%以上把握认为“生二胎与年龄有关”,并说明理由;
(2)以这100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,记其中打算生二胎的人数为X,求随机变量X的分布列,数学期望E(X)和方差D(X). 参考公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
( ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.若p:?x∈R,x2﹣x+1≥0,则¬p:?x∈R,x2﹣x+1<0
B.“ ![]() ”是“θ=30°或θ=150°”的充分不必要条件
”是“θ=30°或θ=150°”的充分不必要条件
C.命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0”
D.已知p:?x∈R,cosx=1,q:?x∈R,x2﹣x+2>0,则“p∧(¬q)”为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=e1﹣x(﹣a+cosx),a∈R.
(Ⅰ)若函数y=f(x)在[0,π]存在单调增区间,求实数a的取值范围;
(Ⅱ)若f( ![]() )=0,证明:对于x∈[﹣1,
)=0,证明:对于x∈[﹣1, ![]() ],总有f(﹣x﹣1)+2f′(x)cos(﹣x﹣1)>0.
],总有f(﹣x﹣1)+2f′(x)cos(﹣x﹣1)>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com