
 (n=2,3,4,…). 在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…,点B1的坐标为(3,3),且
(n=2,3,4,…). 在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…,点B1的坐标为(3,3),且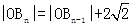 (n=2,3,4,…).
(n=2,3,4,…). ;
; 面积的最大值.
面积的最大值.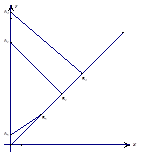
 =
=
 ,∴Bn的坐标为(2n+1,2n+1)
,∴Bn的坐标为(2n+1,2n+1)  .
.  ,
, (n=2,3,4,…), 知
(n=2,3,4,…), 知 (n=2,3,4,…),组成以9为首项,3为公比的等比数列,所以
(n=2,3,4,…),组成以9为首项,3为公比的等比数列,所以 =
= ;
; ,由(1)和在y轴的正半轴上依次有点A1,A2,…,An,…,得
,由(1)和在y轴的正半轴上依次有点A1,A2,…,An,…,得 ,
, ;由
;由 ,
,
 为首项,
为首项, 为公差的等差数列;利用等差数列的通项公式得
为公差的等差数列;利用等差数列的通项公式得 ,即得Bn的坐标;(3)把四边形
,即得Bn的坐标;(3)把四边形 面积分成两个三角形的面积的差,根据三角形的面积公式和(2)可求得,研究数列的单调性得到最大值.
面积分成两个三角形的面积的差,根据三角形的面积公式和(2)可求得,研究数列的单调性得到最大值. ,
, =
= ……………………………………4分
……………………………………4分
 , ……………………………………6分
, ……………………………………6分 ,
,
 为首项,
为首项, 为公差的等差数列
为公差的等差数列

 ,即Sn+1<Sn,
,即Sn+1<Sn, .
.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源:不详 题型:解答题
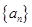 :
: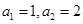 ,且对任意正整数
,且对任意正整数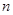 ,有
,有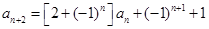 .
.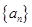 的通项公式与前
的通项公式与前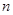 项和
项和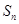 ;
;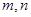 ,使得
,使得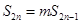 ?若存在,则求出所有的正整数对
?若存在,则求出所有的正整数对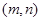 ;若不存在,则加以证明.
;若不存在,则加以证明.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、 、…、
、…、
 是曲线
是曲线 :
: 上的
上的 个点,点
个点,点 (
( )在
)在 轴的正半轴上,且
轴的正半轴上,且 是正三角形(
是正三角形( 是坐标原点).
是坐标原点). 、
、 、
、 ;
; (
( )的横坐标
)的横坐标 关于
关于 的表达式并证明.
的表达式并证明.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
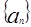 满足
满足 ,则称数列
,则称数列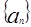 为“等方比数列”甲:数列
为“等方比数列”甲:数列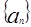 为“等比数列”;乙:数列
为“等比数列”;乙:数列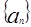 为“等方比数列”;则
为“等方比数列”;则| A.甲是乙的充分不必要条件, |
| B.甲是乙的必要不充分条件, |
| C.甲是乙的充要条件, |
| D.甲既不是乙的充分条件也不是乙的必要条件, |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com