Question

【题目】如图1，在直角梯形ABCP中，CP∥AB，CP⊥CB，AB=BC= CP=2，D是CP的中点，将△PAD沿AD折起，使得PD⊥CD．

（Ⅰ）若E是PC的中点，求证：AP∥平面BDE；
（Ⅱ）求证：平面PCD⊥平面ABCD；
（Ⅲ）求二面角A﹣PB﹣C的大小．

Answer 1

【答案】证明：（Ⅰ）连接AC交BD于点O，连接OE， 在正方形ABCD中，O为AC的中点，又因为E为PC的中点，
所以OE为△PAC的中位线，
所以OE∥AP，
又因为OE平面BDE，AP平面BDE，
所以AP∥平面BDE．
（Ⅱ）由已知可得AD⊥PD，AD⊥CD，
又因为PD∩CD=D，PD，CD平面PCD，
所以AD⊥平面PCD，
又因为AD平面ABCD，
所以平面PCD⊥平面ABCD．
解：（Ⅲ）由（Ⅱ）知AD⊥平面PCD，所以AD⊥PD，又因为PD⊥CD，且AD∩CD=D，
所以PD⊥平面ABCD，
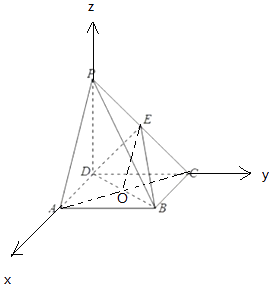
所以以D为坐标原点，DA，DC，DP所在直线分别为x，y，z轴，建立空间直角坐标系，
则P（0，0，2），A（2，0，0），B（2，2，0），C（0，2，0），
所以 ， ，
设平面APB的一个法向量为 ，
所以 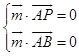即
令a=1，则c=1，从而 ，
同理可求得平面PBC的一个法向量为 ，
设二面角A﹣PB﹣C的大小为θ，易知 ，
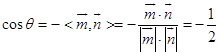所以 ，所以 ，
所以二面角A﹣PB﹣C的大小为 ．

【解析】（Ⅰ）连接AC交BD于点O，连接OE，推导出OE∥AP，由此能证明AP∥平面BDE．（Ⅱ）推导出AD⊥PD，AD⊥CD，从而AD⊥平面PCD，由此能证明平面PCD⊥平面ABCD．（Ⅲ）以D为坐标原点，DA，DC，DP所在直线分别为x，y，z轴，建立空间直角坐标系，利用向量法能求出二面角A﹣PB﹣C的大小．
【考点精析】利用直线与平面平行的判定和平面与平面垂直的判定对题目进行判断即可得到答案，需要熟知平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一个平面过另一个平面的垂线，则这两个平面垂直．