
分析 (Ⅰ)推导出M点轨迹是以A、B为焦点的椭圆,由此能求出动圆圆心M的轨迹C的标准方程.
(Ⅱ)设l:y=kx+b,将l的方程与椭圆C的方程的联立,化简得(1+2k2)x2+4kbx+2b2-2=0,由此利用根的判别式、韦达定理、向量的数量积公式,结合题意能证明$\overrightarrow{OM}$•$\overrightarrow{PQ}$为定值-1.
解答 解:(Ⅰ)设动圆M的半径为r,依题意,|MA|=2$\sqrt{2}$-r,|MB|=r,
∴|MA|+|MB|=2$\sqrt{2}$>|AB|=2,
∴M点轨迹是以A、B为焦点的椭圆,
∴动圆圆心M的轨迹C的标准方程为$\frac{{x}^{2}}{2}$+y2=1.…(5分)
证明:(Ⅱ)由题意可知,直线l的斜率存在且不为0,设l:y=kx+b,
将l的方程与椭圆C的方程的联立,化简得:
(1+2k2)x2+4kbx+2b2-2=0,
因为l与椭圆C相切于点M,设M(x0,y0),
所以△=8(1+2k2-b2)=0,即b2=1+2k2,
且2x0=-$\frac{4kb}{1+2{k}^{2}}$=-$\frac{4kb}{{b}^{2}}$,解得x0=-$\frac{2k}{b}$,y0=-$\frac{2{k}^{2}}{b}$+b=$\frac{1}{b}$,
∴点M的坐标为(-$\frac{2k}{b}$,$\frac{1}{b}$),
又l与x轴、y轴分别交于P、Q两点,
∴点P的坐标为(-$\frac{b}{k}$,0),点Q的坐标为(0,b),$\overrightarrow{PQ}$=($\frac{b}{k}$,b),
∴$\overrightarrow{OM}$•$\overrightarrow{PQ}$=(-$\frac{2k}{b}$,$\frac{1}{b}$)•($\frac{b}{k}$,b)=-1.
∴$\overrightarrow{OM}$•$\overrightarrow{PQ}$为定值-1.…(12分)
点评 本题考查点的轨迹方程的求法,考查向量的数量积为定值的证明,是中档题,解题时要认真审题,注意根的判别式、韦达定理、向量的数量积公式、圆、椭圆等知识点的合理运用.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
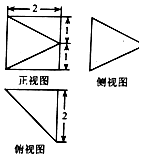
| A. | $\frac{8}{3}$ | B. | 4$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-8]∪[0,+∞) | B. | (-8,0) | C. | (-∞,0] | D. | [-8,0] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com