
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,把函数
)的部分图象如图所示,把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移1个单位,得到函数
个单位长度,再向下平移1个单位,得到函数![]() 的图像.
的图像.

(1)当![]() 时,求
时,求![]() 的值域
的值域
(2)令![]() ,若对任意
,若对任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】每当《我心永恒》这首感人唯美的歌曲回荡在我们耳边时,便会想起电影《泰坦尼克号》中一暮暮感人画面,让我们明白了什么是人类的“真、善、美”.为了推动我市旅游发展和带动全市经济,更为了向外界传递遂宁人民的“真、善、美”.我市某地将按“泰坦尼克号”原型![]() 比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市
比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
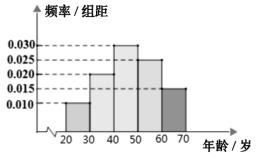
(1)求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄在
人,求所抽取的人中恰好没有年龄在![]() 段的概率.
段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将![]() 的方程化为普通方程,将
的方程化为普通方程,将![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数,且
为参数,且![]() ),
),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人经营一个抽奖游戏,顾客花费3元钱可购买一次游戏机会,每次游戏中,顾客从标有黑1、黑2、黑3、黑4、红1、红3的6张卡片中随机抽取2张,并根据摸出的卡片的情况进行兑奖,经营者将顾客抽到的卡片情况分成以下类别:![]() :同花顺,即卡片颜色相同且号码相邻;
:同花顺,即卡片颜色相同且号码相邻;![]() :同花,即卡片颜色相同,但号码不相邻;
:同花,即卡片颜色相同,但号码不相邻;![]() :顺子,即卡片号码相邻,但颜色不同;
:顺子,即卡片号码相邻,但颜色不同;![]() :对子,即两张卡片号码相同;
:对子,即两张卡片号码相同;![]() :其它,即
:其它,即![]() ,
,![]() ,
,![]() ,
,![]() 以外的所有可能情况,若经营者打算将以上五种类别中最不容易发生的一种类别对应顾客中一等奖,最容易发生的一种类别对应顾客中二等奖,其他类别对应顾客中三等奖.
以外的所有可能情况,若经营者打算将以上五种类别中最不容易发生的一种类别对应顾客中一等奖,最容易发生的一种类别对应顾客中二等奖,其他类别对应顾客中三等奖.
(1)一、二等奖分别对应哪一种类别?(写出字母即可)
(2)若经营者规定:中一、二、三等奖,分别可获得价值9元、3元、1元的奖品,假设某天参与游戏的顾客为300人次,试估计经营者这一天的盈利.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行跳棋比赛,约定每局胜者得1分,负者得0分.若其中的一方比对方多得2分或下满5局时停止比赛.设甲在每局中获胜的概率为![]() ,乙在每局中获胜的概率为
,乙在每局中获胜的概率为![]() ,且各局胜负相互独立.
,且各局胜负相互独立.
(1)求没下满5局甲就获胜的概率;
(2)设比赛结束时已下局数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,且短轴长为6.
,且短轴长为6.
(1)求椭圆的标准方程;
(2)是否存在斜率为1的直线l,使得l与曲线C相交于A,B两点,且以AB为直径的圆恰好经过原点?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)
已知抛物线![]() 的焦点F与椭圆
的焦点F与椭圆![]() 的一个焦点重合,点
的一个焦点重合,点![]() 在抛物线上,过焦点F的直线l交抛物线于A,B两点.
在抛物线上,过焦点F的直线l交抛物线于A,B两点.
(1)求抛物线C的标准方程以及![]() 的值.
的值.
(2)记抛物线的准线![]() 轴交于点H,试问是否存在常数
轴交于点H,试问是否存在常数![]() ,使得
,使得![]() ,且
,且![]() 都成立.若存在,求出
都成立.若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区发现某污染源,相关部门对污染情况进行调查研究后,发现一天中污染指数![]() 与时刻x(时)的函数关系为
与时刻x(时)的函数关系为![]() ,其中a是与气象有关的参数,且
,其中a是与气象有关的参数,且![]() .按规定,若每天污染指数不超过2,则环保合格,否则需要整改.如果以每天中
.按规定,若每天污染指数不超过2,则环保合格,否则需要整改.如果以每天中![]() 的最大值作为当天的污染指数,并记为
的最大值作为当天的污染指数,并记为![]() ,那么该地区污染指数的超标情况为________.
,那么该地区污染指数的超标情况为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数图象的有下列说法:
①若函数![]() 满足
满足![]() ,则
,则![]() 的一个周期为
的一个周期为![]() ;
;
②若函数![]() 满足
满足![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
③函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④若函数![]() 与函数
与函数![]() 的图象关于原点对称,则
的图象关于原点对称,则![]() ,
,
其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com