
| A. | $-\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $-\frac{1}{3}$ | D. | 1 |
分析 由于本题是选择题,不妨设△ABC为等边三角形,由题意可得F是△ABC的重心,即可得到$\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{EC}$=-$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$,继而求出λ,μ的值,问题得以解决.
解答 解:不妨设△ABC为等边三角形,D是BC中点,E是AB中点,CE交AD于点F,
∴F是△ABC的重心,
∴$\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{EC}$=$\frac{1}{3}$($\overrightarrow{EB}$+$\overrightarrow{BC}$)=$\frac{1}{3}$($\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{AC}$-$\overrightarrow{AB}$)=-$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$,
∵$\overrightarrow{EF}=λ\overrightarrow{AB}+u\overrightarrow{AC}$,
∴λ=-$\frac{1}{6}$,μ=$\frac{1}{3}$,
∴λ+μ=$\frac{1}{6}$,
故选:B.
点评 本题考查代数和的求法,是基础题,解题时要认真审题,注意平面向量的加法法则的合理运用


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | AB•AC=$\sqrt{2}$AB+AC | B. | AB+AC=$\sqrt{2}$AB•AC | C. | AB•AC=$\sqrt{3}$AB+AC | D. | AB+AC=$\sqrt{3}$AB•AC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{25}$ | B. | $\frac{24}{25}$ | C. | $-\frac{24}{25}$ | D. | $-\frac{12}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
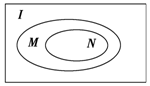
| A. | (∁IM)?(∁IN) | B. | M⊆(∁IN) | C. | (∁IM)⊆(∁IN) | D. | M?(∁IN) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x>1,则$\frac{1}{x}$<1”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com