
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
试题(Ⅰ)连接AC1交A1C于点F,则DF为三角形ABC1的中位线,故DF∥BC1.再根据直线和平面平行的判定定理证得BC1∥平面A1CD.(Ⅱ)由题意可得此直三棱柱的底面ABC为等腰直角三角形,由D为AB的中点可得CD⊥平面ABB1A1.求得CD的值,利用勾股定理求得A1D、DE和A1E的值,可得A1D⊥DE.进而求得S△A1DE的值,再根据三棱锥C-A1DE的体积为![]() S△A1DECD,运算求得结果
S△A1DECD,运算求得结果
试题解析:(1)证明:连结AC1交A1C于点F,则F为AC1中点又D是AB中点,
连结DF,则BC1∥DF. 3分
因为DF平面A1CD,BC1不包含于平面A1CD, 4分
所以BC1∥平面A1CD. 5分
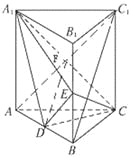
(2)解:因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥CD.由已知AC=CB,D为AB的中点,所以CD⊥AB.又AA1∩AB=A,于是CD⊥平面ABB1A1. 8分
由AA1=AC=CB=2,![]() 得∠ACB=90°,
得∠ACB=90°,![]() ,
,![]() ,
,![]() ,A1E=3,故A1D2+DE2=A1E2,即DE⊥A1D 10分
,A1E=3,故A1D2+DE2=A1E2,即DE⊥A1D 10分
所以三菱锥C﹣A1DE的体积为:![]() =
=![]() =1. 12分
=1. 12分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°, ![]() .
. 
(1)证明:DC⊥AB;
(2)若点C在平面ABDE内的射影H,求CH与平面BCD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市组织了一次高二调研考试,考试后统计的数学成绩服从正态分布,其密度函数![]() , x∈(-∞,+∞),则下列命题不正确的是( )
, x∈(-∞,+∞),则下列命题不正确的是( )
A. 该市这次考试的数学平均成绩为80分
B. 分数在120分以上的人数与分数在60分以下的人数相同
C. 分数在110分以上的人数与分数在50分以下的人数相同
D. 该市这次考试的数学成绩标准差为10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex(x3﹣3x+3)﹣aex﹣x(x≥﹣2),若不等式f(x)≤0有解,则实数α的最小值为( )
A.![]()
B.2﹣ ![]()
C.1﹣ ![]()
D.1+2e2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C的方程为 ![]() ,点
,点 ![]() ,以极点为原点,极轴为x轴的正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
,以极点为原点,极轴为x轴的正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(1)求曲线C的直角坐标方程及点R的直角坐标;
(2)设P为曲线C上一动点,以PR为对角线的矩形PQRS的一边垂直于极轴,求矩形PQRS周长的最小值及此时点P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴非负半轴重合,直线![]() 的极坐标方程为
的极坐标方程为![]() ,圆C的参数方程为
,圆C的参数方程为![]() ,
,
(1)求直线![]() 被圆C所截得的弦长;
被圆C所截得的弦长;
(2)已知点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆所相交于
与圆所相交于![]() 不同的两点,求
不同的两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对某种食材营养价值的认识程度,某档健康养生电视节目组织![]() 名营养专家和
名营养专家和![]() 名现场观众各组成一个评分小组,给食材的营养价值打分(十分制).下面是两个小组的打分数据:
名现场观众各组成一个评分小组,给食材的营养价值打分(十分制).下面是两个小组的打分数据:
第一小组 |
|
|
|
|
|
|
|
|
第二小组 |
|
|
|
|
|
|
|
|

(1)求第一小组数据的中位数与平均数,用这两个数字特征中的哪一种来描述第一小组打分的情况更合适?说明你的理由.
(2)你能否判断第一小组与第二小组哪一个更像是由营养专家组成的吗?请比较数字特征并说明理由.
(3)节目组收集了烹饪该食材的加热时间:(单位:![]() )与其营养成分保留百分比
)与其营养成分保留百分比![]() 的有关数据:
的有关数据:
食材的加热时间 |
|
|
|
|
|
|
营养成分保留百分比 |
|
|
|
|
|
|
在答题卡上画出散点图,求![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ),并说明回归方程中斜率
),并说明回归方程中斜率![]() 的含义.
的含义.
附注:参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com