
分析 ①,$\frac{1}{x}≠0$,∴函数$y={0.7^{\frac{1}{x}}}$≠1;
②,a=0时,直线2x+ay-1=0与直线(a-1)x-ay-1=0也平行;
③,过点A(1,2)且在坐标轴上的截距相等的直线还有过原点的直线;
④,利用公式求出圆柱的侧面积即可.
解答 解:对于①,∵$\frac{1}{x}≠0$,∴函数$y={0.7^{\frac{1}{x}}}$的值域是(0,1)∪(1,+∞),故错;
对于②,直线2x+ay-1=0与直线(a-1)x-ay-1=0平行,则a=-1或0,故错;
对于③,过点A(1,2)且在坐标轴上的截距相等的直线的方程为x+y=3或y=2x,故错;
对于④,若圆柱的底面直径与高都等于球的直径2r,则圆柱的侧面积等于2πr•2r=4πr2等于球的表面积,故正确.
故答案为:④
点评 本题考查了命题真假的判定,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 同学们做不出符合要求的三角形 | B. | 能做出一个锐角三角形 | ||
| C. | 能做出一个直角三角形 | D. | 能做出一个钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
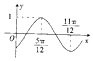 已知函数f(x)=sin(ωx+φ)(ω>0,π<|φ|<,2π)的部分图象如图所示,则φ的值为( )
已知函数f(x)=sin(ωx+φ)(ω>0,π<|φ|<,2π)的部分图象如图所示,则φ的值为( )| A. | $\frac{5π}{3}$ | B. | $\frac{4π}{3}$ | C. | -$\frac{4π}{3}$ | D. | -$\frac{5π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\root{3}{x^3}$ | B. | $y={(\sqrt{x})^2}$ | C. | $y=\sqrt{x^2}$ | D. | $y=\frac{x^2}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
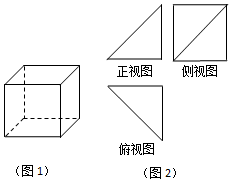
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com