
【题目】3名男生、3名女生站成一排:
(1)女生都不站在两端,有多少不同的站法?
(2)三名男生要相邻,有多少种不同的站法?
(3)三名女生互不相邻,三名男生也互不相邻,有多少种不同的站法?
(4)女生甲,女生乙都不与男生丙相邻,有多少种不同的站法?
【答案】(1)144.
(2)144.
(3)72.
(4)288.
【解析】分析:(1)中间的4个位置任选3个排女生,其余3个位置任意排男生,问题得以解决;
(2)利用捆绑法,先把3个男生捆绑在一起看做一个复合元素,再和3个女生做全排列;
(3)利用插空法,把3名女生插入到3名男生形成的四个空中连续地插入3名女生有2种方法,即可得到答案;
(4)分两类,第一类男生丙在两端,第二类男生丙不在两端,根据分类计数原理可得.
详解:(1).中间的4个位置任选3个排女生,其余3个位置任意排男生:![]() (种);
(种);
(2).把3名男生当作一个元素,于是对3个元素任意排,然后和3个女生做全排列: ![]() (种);
(种);
(3).把男生任意全排列,在产生的四个空中连续地插入3名女生有2种方法:![]() (种);
(种);
(4).按男生丙在两端和不在两端分类,
第一类,男生丙在两端时,从除甲乙丙外的三人中选择一人填充男生丙邻位,其余4人做任意排列:![]() .
.
第二类,男生丙不在两端时,从除甲乙丙外的三人中选择2人填充男生丙邻位,其余三人做任意排列:![]() ,
,
共有方法:![]() +
+![]() =288(种)
=288(种)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,解不等式
,解不等式![]() ;
;
(Ⅱ)设![]() 是函数
是函数![]() 的四个不同的零点,问是否存在实数
的四个不同的零点,问是否存在实数![]() ,使得其中三个零点成等差数列?若存在,求出所有
,使得其中三个零点成等差数列?若存在,求出所有![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx),其中常数ω>0
(1)令ω=1,判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)令ω=2,将函数y=f(x)的图象向左平移个![]() 单位,再向上平移1个单位,得到函数y=g(x)的图象,对任意a∈R,求y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
单位,再向上平移1个单位,得到函数y=g(x)的图象,对任意a∈R,求y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:
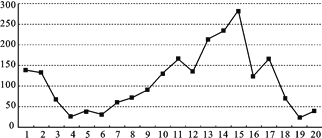
下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x﹣1)的图象关于点(1,0)对称,且当x∈(﹣∞,0)时,f(x)+xf′(x)<0成立(其中f′(x)是f(x)的导函数),若a=(30.3)f(30.3),b=(logπ3)f(logπ3),c=(log3 ![]() )f(log3
)f(log3 ![]() ),则 a,b,c的大小关系是( )
),则 a,b,c的大小关系是( )
A.a>b>c
B.c>a>b
C.c>b>a
D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世界卫生组织设定的最宽限值,即
标准采用世界卫生组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的![]() 监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).
监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).

(1)求这18个数据中不超标数据的平均数与方差;
(2)在空气质量为一级的数据中,随机抽取2个数据,求其中恰有一个为![]() 日均值小于30微克/立方米的数据的概率;
日均值小于30微克/立方米的数据的概率;
(3)以这![]() 天的
天的![]() 日均值来估计一年的空气质量情况,则一年(按
日均值来估计一年的空气质量情况,则一年(按![]() 天计算)中约有多少天的空气质量超标.
天计算)中约有多少天的空气质量超标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com