
【题目】已知椭圆C:![]() (
(![]() )的焦距等于短轴的长,椭圆的右顶点到左焦点
)的焦距等于短轴的长,椭圆的右顶点到左焦点![]() 的距离为
的距离为![]() .
.
(1)求椭圆C的标准方程;
(2)已知直线l:![]() (
(![]() )与椭圆C交于A、B两点,在y轴上是否存在点
)与椭圆C交于A、B两点,在y轴上是否存在点![]() ,使得
,使得![]() ,且
,且![]() ,若存在,求实数t的取值范围;若不存在,请说明理由.
,若存在,求实数t的取值范围;若不存在,请说明理由.
【答案】(1)![]() (2)存在,
(2)存在,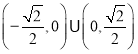
【解析】
(1)由题意可得![]() 的关系,解方程组求得
的关系,解方程组求得![]() ,即可得椭圆的标准方程.
,即可得椭圆的标准方程.
(2)设![]() ,
,![]() ,联立直线与椭圆方程,用韦达定理表示出
,联立直线与椭圆方程,用韦达定理表示出![]() ,
,![]() ,利用弦长公式表示出
,利用弦长公式表示出![]() .化简后用
.化简后用![]() 表示出
表示出![]() ,再通过判别式判断出
,再通过判别式判断出![]() 的取值范围. 设出
的取值范围. 设出![]() 中点
中点![]() 的坐标,由点斜式表示出直线
的坐标,由点斜式表示出直线![]() 的方程,并令
的方程,并令![]() 求得
求得![]() 的表达式及取值范围即可.
的表达式及取值范围即可.
(1)依题意椭圆的焦距等于短轴的长,椭圆的右顶点到左焦点![]() 的距离为
的距离为![]()
可得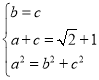 ,
,
解得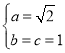 ,
,
所以所求椭圆方程为![]() ;
;
(2)设![]() ,
,![]() ,
,
由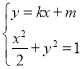 ,
,
得![]() ,
,
![]() ,
,
∵![]() ,
,![]() ,
,
假设存在点![]() 满足题意,
满足题意,
![]()
![]() ,
,
化简整理得 ,
,
此时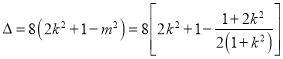
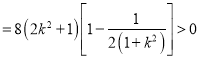 恒成立,
恒成立,
所以![]() 且
且![]() ,
,
设![]() 中点
中点![]() ,
,
则![]() ,
,![]() ,
,
由![]() ,则
,则![]() 在线段AB的中垂线上.
在线段AB的中垂线上.
因为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,则
,则![]() ,
,
∴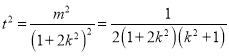 ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
综上,存在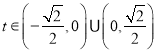 满足题意.
满足题意.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】某幼儿园举办“yue”主题系列活动——“悦”动越健康亲子运动打卡活动,为了解小朋友坚持打卡的情况,对该幼儿园所有小朋友进行了调查,调查结果如下表:
打卡天数 | 17 | 18 | 19 | 20 | 21 |
男生人数 | 3 | 5 | 3 | 7 | 2 |
女生人数 | 3 | 5 | 5 | 7 | 3 |
(1)根据上表数据,求该幼儿园男生平均打卡的天数;
(2)若从打卡21天的小朋友中任选2人交流心得,求选到男生和女生各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,设直线
,设直线![]() ,其中
,其中![]() ,给出下列结论:
,给出下列结论:
①直线![]() 的方向向量与向量
的方向向量与向量![]() 共线;
共线;
②若![]() ,则直线
,则直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ;
;
③直线![]() 与直线
与直线![]() (
(![]() )一定平行;
)一定平行;
写出所有真命题的序号________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() 是以坐标原点
是以坐标原点![]() 为顶点,直线
为顶点,直线![]() 为准线的抛物线.以坐标原点
为准线的抛物线.以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系.
轴非负半轴为极轴建立极坐标系.
(1)分别求出直线![]() 与曲线
与曲线![]() 的极坐标方程:
的极坐标方程:
(2)点![]() 是曲线
是曲线![]() 上位于第一象限内的一个动点,点
上位于第一象限内的一个动点,点![]() 是直线
是直线![]() 上位于第二象限内的一个动点,且
上位于第二象限内的一个动点,且![]() ,请求出
,请求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,左、右两顶点分别是
,左、右两顶点分别是![]() 、
、![]() ,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点
,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点![]() 如图).
如图).
⑴若![]() 是
是![]() 的一条渐近线的一个方向向量,试求
的一条渐近线的一个方向向量,试求![]() 的两渐近线的夹角
的两渐近线的夹角![]() ;
;
⑵若![]() ,
,![]() ,
,![]() ,
,![]() ,试求双曲线
,试求双曲线![]() 的方程;
的方程;
⑶在⑴的条件下,且![]() ,点C与双曲线的顶点不重合,直线
,点C与双曲线的顶点不重合,直线![]() 和直线
和直线![]() 与直线l:
与直线l:![]() 分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂预购软件服务,有如下两种方案:
方案一:软件服务公司每日收取工厂60元,对于提供的软件服务每次10元;
方案二:软件服务公司每日收取工厂200元,若每日软件服务不超过15次,不另外收费,若超过15次,超过部分的软件服务每次收费标准为20元.
(1)设日收费为![]() 元,每天软件服务的次数为
元,每天软件服务的次数为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该工厂对过去100天的软件服务的次数进行了统计,得到如图所示的条形图,依据该统计数据,把频率视为概率,从节约成本的角度考虑,从两个方案中选择一个,哪个方案更合适?请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
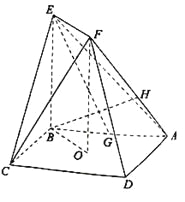
(Ⅰ)求证:EG∥平面ADF;
(Ⅱ)求二面角OEFC的正弦值;
(Ⅲ)设H为线段AF上的点,且AH=![]() HF,求直线BH和平面CEF所成角的正弦值.
HF,求直线BH和平面CEF所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com