
【题目】有四名男生,三名女生排队照相,七个人排成一排,则下列说法正确的有( )
A.如果四名男生必须连排在一起,那么有![]() 种不同排法
种不同排法
B.如果三名女生必须连排在一起,那么有![]() 种不同排法
种不同排法
C.如果女生不能站在两端,那么有![]() 种不同排法
种不同排法
D.如果三个女生中任何两个均不能排在一起,那么有![]() 种不同排法
种不同排法
【答案】CD
【解析】
利用捆绑法可计算出A、B选项中的排法种数,利用特殊位置法可计算出C选项中的排法种数,利用插空法可计算出D选项中的排法种数,综合可得出结果.
A中,如果四名男生必须连排在一起,将这四名男生捆绑,形成一个“大元素”,此时,共有![]() 种不同的排法,A选项错误;
种不同的排法,A选项错误;
B中,如果三名女生必须连排在一起,将这三名女生捆绑,形成一个“大元素”,此时,共有![]() 种不同的排法种数,B选项错误;
种不同的排法种数,B选项错误;
C中,如果女生不能站在两端,则两端安排男生,其他位置的安排没有限制,此时,共有![]() 种不同的排法种数,C选项正确;
种不同的排法种数,C选项正确;
D中,如果三个女生中任何两个均不能排在一起,将女生插入四名男生所形成的![]() 个空中,此时,共有
个空中,此时,共有![]() 种不同的排法种数,D选项正确.
种不同的排法种数,D选项正确.
故选:CD.


科目:高中数学 来源: 题型:
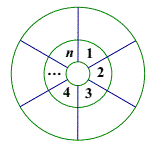
【题目】如图所示将同心圆环均匀分成n(![]() )格.在内环中固定数字1~n.问能否将数字1~n填入外环格内,使得外环旋转任意格后有且仅有一个格中内外环的数字相同?
)格.在内环中固定数字1~n.问能否将数字1~n填入外环格内,使得外环旋转任意格后有且仅有一个格中内外环的数字相同?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一商家诚邀甲、乙两名围棋高手进行一场网络国棋比赛,每比赛一局商家要向每名棋手支付2000元对局费,同时商家每局从转让网络转播权及广告宣传中获利12100元,从两名棋手以往比赛中得知,甲每局获胜的概率为![]() ,乙每局获胜的概率为
,乙每局获胜的概率为![]() ,两名棋手约定:最多下五局,先连胜两局者获胜,比赛结束,比赛结束后,商家为获胜者颁发5000元的奖金,若没有决出获胜者则各颁发2500元.
,两名棋手约定:最多下五局,先连胜两局者获胜,比赛结束,比赛结束后,商家为获胜者颁发5000元的奖金,若没有决出获胜者则各颁发2500元.
(1)求下完五局且甲获胜的概率是多少;
(2)求商家从这场网络棋赛中获得的收益的数学期望是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某景区内有两条道路![]() 、
、![]() ,现计划在
,现计划在![]() 上选择一点
上选择一点![]() ,新建道路
,新建道路![]() ,并把
,并把![]() 所在的区域改造成绿化区域.已知
所在的区域改造成绿化区域.已知![]() ,
,![]() ,
,![]() .若绿化区域
.若绿化区域![]() 改造成本为
改造成本为![]() 万元
万元![]() ,新建道路
,新建道路![]() 成本为
成本为![]() 万元
万元![]() .
.
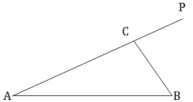
(1)①设![]() ,写出该计划所需总费用
,写出该计划所需总费用![]() 的表达式,并写出
的表达式,并写出![]() 的范围;
的范围;
②设![]() ,写出该计划所需总费用
,写出该计划所需总费用![]() 的表达式,并写出
的表达式,并写出![]() 的范围;
的范围;
(2)从上面两个函数关系中任选一个,求点![]() 在何处时改造计划的总费用最小.
在何处时改造计划的总费用最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
求甲在4局以内(含4局)赢得比赛的概率;
记![]() 为比赛决出胜负时的总局数,求
为比赛决出胜负时的总局数,求![]() 的分布列和均值(数学期望).
的分布列和均值(数学期望).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com